Question: Recursion problem A Continued fraction is an expression which has the form of (see picture) Write a python function using recursion only Continued_f(n, i) consumes

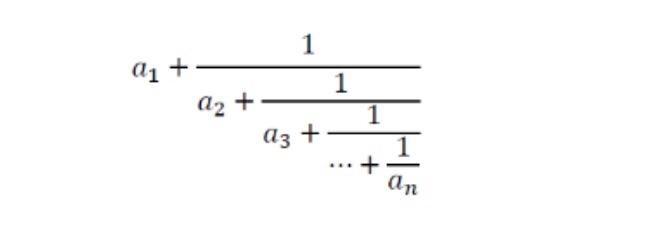
A Continued fraction is an expression which has the form of 1 a + Q2 + a3 + an Write a python function using recursion only Continued fin, 0) consumes a positive number n and (a total number of iteration times which is a positive integer). The final anawer should ha formatted as a string and should end with a fult lop() after the last value Continued. (1.76, 21:11 Continued.1017/14,5) 1:41.2.1 To compute a continued froction for n, weiterate through these steps: 1. It is an integer, addit it to the end of the string and return 2. If n is not an integer, round n down to its nearest Integer (floor function is useful) Subtract this integer from This value is the included in the final answer 3. The provious steps are repeated with the reciprocal of this number. Stop when you've performed this a total of number of times or until you hit an integer. For example, w17/14, 1-5 we start with the first integer 1, subtract it from 17/14 to get 3/14, and take the reciprocol 14/3 and repeat the process. 1/3 has the integer part 4 and subtract from 14/3 to get 2/3. Then take the reciprocal and get 3/2, 3/2 has the integer port 1 and subtract from 3/2 to get 1/2 take the reciprocal to get 2. This is an integer and hence we are done. The continued traction is 11:4, 1,2 1 1 + a2 + 1 1 + + an
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


