Rederive the expression for the Forward rate F(t,T1,T2).

Starting from this expression:

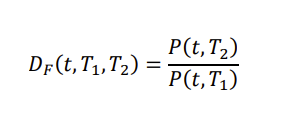
But, now assuming continuous compounding (e.g., of the form: exp(-rT) rather than of the form: 1/(1+rT)) for the forward starting discounting DF using the constant forward rate F(t,T1,T2), between T1 and T2, restate the expression of the Forward Rate w.r.t. to the Bond Prices. Show that as = T2-T1, tends to zero (instantaneous forward), both expressions ( simple compounding vs continuous compounding you restated above) converge to the same result.

DF(t,T1,T2)=P(t,T1)P(t,T2)