Question: Refer to Table S6.1 - Factors for Computing_Control Chart Limits (3 sigma) for this problem. Twelve samples, each containing five parts, were taken from a

from a process that produces steel rods at Emmanual Kodzi': factory. The

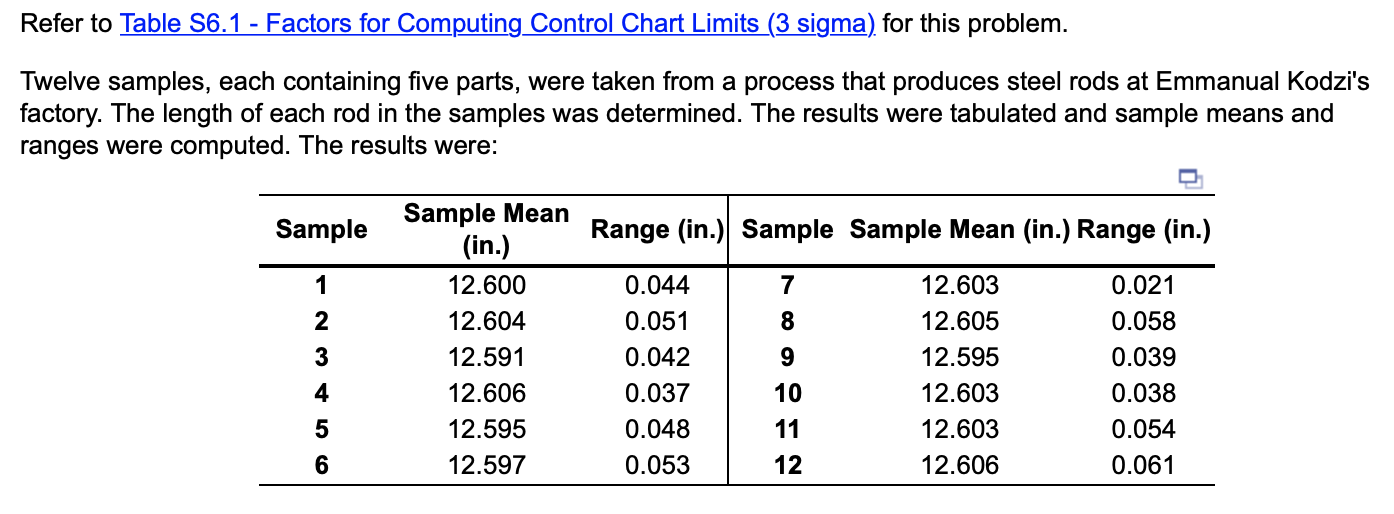
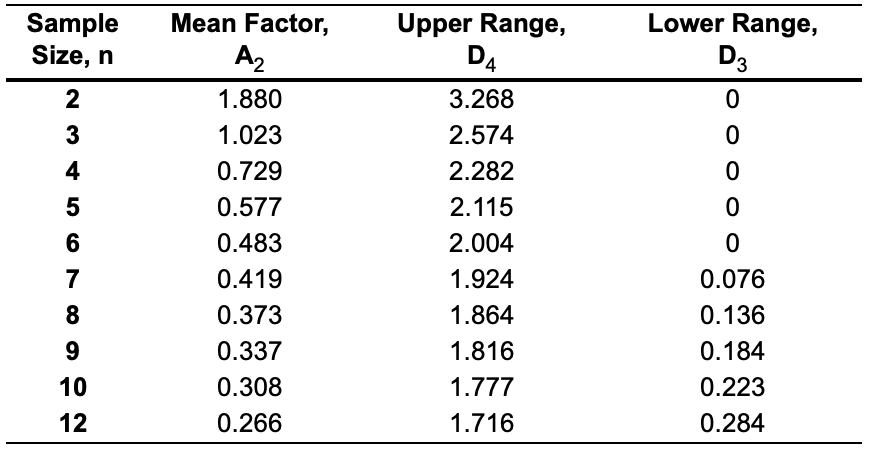
Refer to Table S6.1 - Factors for Computing_Control Chart Limits (3 sigma) for this problem. Twelve samples, each containing five parts, were taken from a process that produces steel rods at Emmanual Kodzi': factory. The length of each rod in the samples was determined. The results were tabulated and sample means and ranges were computed. The results were: \begin{tabular}{cccc} \hline SampleSize,n & MeanFactor,A2 & UpperRange,D4 & LowerRange,D3 \\ \hline 2 & 1.880 & 3.268 & 0 \\ 3 & 1.023 & 2.574 & 0 \\ 4 & 0.729 & 2.282 & 0 \\ 5 & 0.577 & 2.115 & 0 \\ 6 & 0.483 & 2.004 & 0 \\ 7 & 0.419 & 1.924 & 0.076 \\ 8 & 0.373 & 1.864 & 0.136 \\ 9 & 0.337 & 1.816 & 0.184 \\ 10 & 0.308 & 1.777 & 0.223 \\ 12 & 0.266 & 1.716 & 0.284 \\ \hline \end{tabular} For the given data, the x= inches (round your response to four decimal places). Based on the sampling done, the control limits for 3-sigma x chart are: Upper Control Limit (UCL)= inches (round your response to four decimal places). Lower Control Limit (LCL)= inches (round your response to four decimal places). Based on the x-chart, is one or more samples beyond the control limits? For the given data, the R= inches (round your response to four decimal places). The control limits for the 3-sigma R-chart are: Upper Control Limit (UCLR)= inches (round your response to four decimal places). Lower Control Limit (LCLR)= inches (round your response to four decimal places). Based on the R-chart, is one or more samples beyond the control limits

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related General Management Questions!

Refer to Table S6.1 - Factors for Computing_Control Chart Limits ( 3 sigma) for this problem. Twelve samples, each containing five parts, were taken from a process that produces steel rods at...

Refer to Table $6.1 - Factors for Computing_Control Chart Limits ( 3 sigma) for this problem. Twelve samples, each containing five parts, were taken from a process that produces steel rods at...

Refer to Table S 6 . 1 - Factors for Computing Control Chart Limits ( 3 sigma ) for this problem. Thirty - five samples of size 7 each were taken from a fertilizer - bag - filling machine at Panos...

Refer to Table S6.1 - Factors for Computing_Control Chart Limits ( 3 sigma) for this problem. Thirty-five samples of size 7 each were taken from a fertilizer-bag-filling machine at Panos Kouvelis...

question 2 Refer to Table S6.1 - Factors for Computing_Control Chart Limits ( 3 sigma) for this problem. Thirty-five samples of size 7 each were taken from a fertilizer-bag-filling machine at Panos...

Refer to Table S6.1 - Factors for Computing_Control Chart Limits (3 sigma) for this problem. Thirty-five samples of size 7 each were taken from a fertilizer-bag-filling machine at Panos Kouvelis...

Please help me solve for part b.) Refer to Table S6.1 - Factors for Computing_Control Chart Limits (3 sigma) for this problem. Thirty-five samples of size 7 each were taken from a...

- Before making month-end adjustments, net income of Bobwhite Company was $232,000 for March. Adjusting entries are necessary for the following items: Depreciation for the month of March: $ 4,300....

As a business valuation expert, you have been allotted with the project to value the company "Top Car S.A.", a used car vehicle vendor that operates a sizable auto spare parts division. The table...

General Accounting Orion Tools Ltd. had gross sales of $72,000 for the year. Its cost of goods sold (COGS) was $42,000, and returns and allowances amounted to $6,000. During the year, Orion Tools...

We have a table below: Please answer the following questions: 1. What is the normal form of the table? Please explain by describing the functional dependency in the table. 2. Normalize this table to...