Question: 1 Let X be the set of infinite sequences a = (ai)ien of real numbers such that |ai| < . For a = (ai)ieN

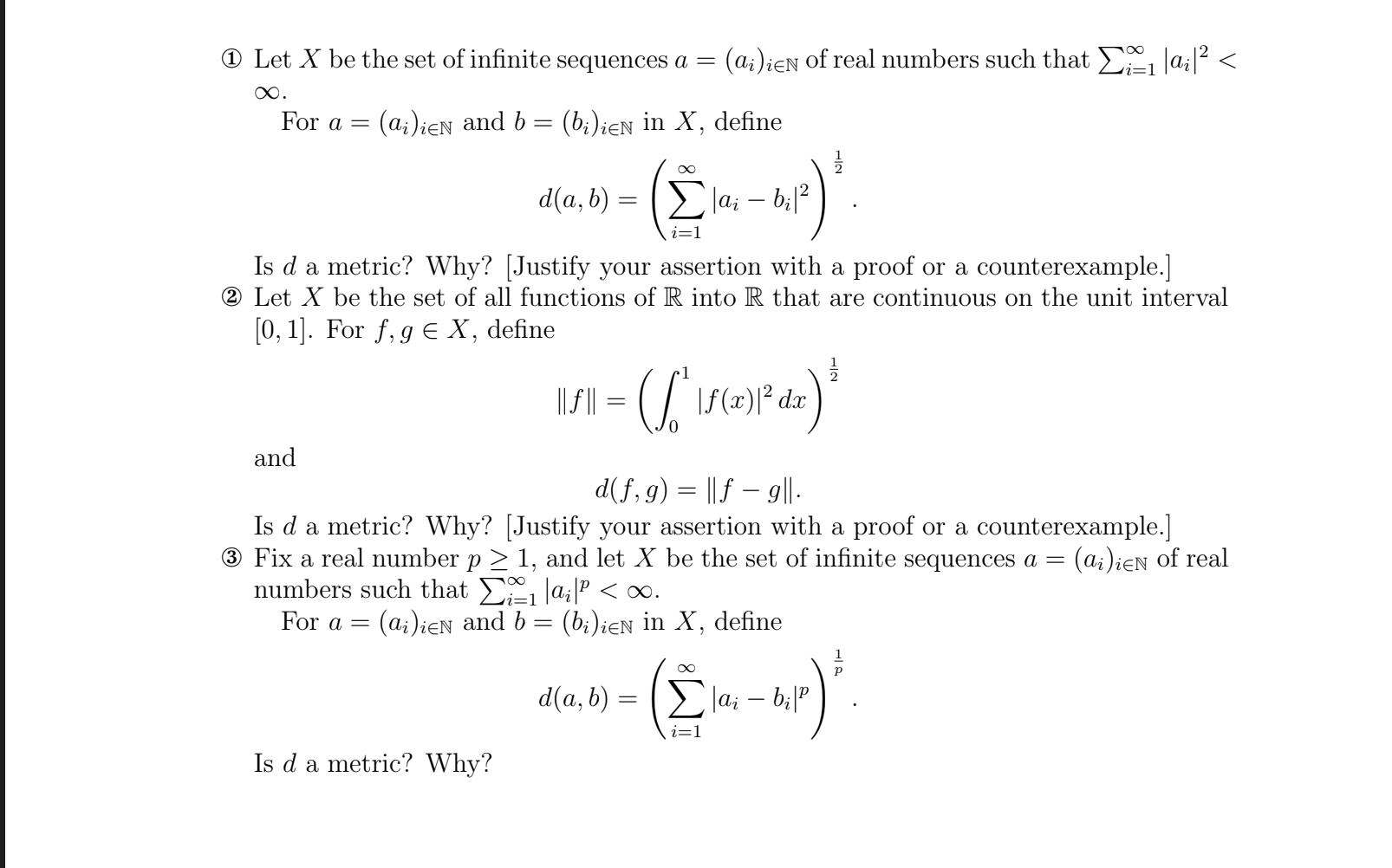
$(1) Let ( X ) be the set of infinite sequences ( a=left(a_{i}ight)_{i in mathbb{N}} ) of real numbers such that ($

1 Let X be the set of infinite sequences a = (ai)ien of real numbers such that |ai| < . For a = (ai)ieN and b = (bi)ien in X, define and d(a, b): Is da metric? Why? [Justify your assertion with a proof or a counterexample.] 2 Let X be the set of all functions of R into R that are continuous on the unit interval [0, 1]. For f, g E X, define (ai)ieN and b lai - b| i=1 Is d a metric? Why? ||*|| = (S |f(x)| dx d(f, g) = || f g||. Is da metric? Why? [Justify your assertion with a proof or a counterexample.] 3 Fix a real number p 1, and let X be the set of infinite sequences a = (ai)ien of real numbers such that a P < 0. For a = (bi)ieN in X, define = 1/1/20 d(a, b) = |ai - bi|P i=1 1/1/201 -^/^)

Step by Step Solution

★★★★★

3.45 Rating (171 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

gons let X be the set of imifinite sequence a an not of real numbers Such that you last ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

Refer to the Buena School District bus data. Information provided by manufacturers of school buses suggests the mean maintenance cost per month is $455 per bus. Use statistical software to find the...

Refer to the Buena school district bus data. Information provided by manufacturers of school buses suggests the mean maintenance cost per month is $455 per bus. Use statistical software to find the...

Refer to the Buena School District bus data. a. Conduct a test of hypothesis to reveal whether the mean maintenance cost is equal for each of the bus manufacturers. Use the .01 significance level. b....

Think of an organization you know something about, and answer the following questions for it: a. Your organization is thinking about developing a knowledge management system that requires workers to...

In this exercise, we construct an example of a sequence of random variables Zn such that but That is, Zn converges in probability to 0, but Zn does not converge to 0 with probability 1. Indeed, Zn...

Let E1 be the unit interval [0, 1] with its middle third (1/3, 2/3) removed (i.e., E1 = [0, l/3]U[2/3, 1]). Let E2 be E1 with its middle thirds removed; that is, E2 = [0, 1/9] U [2/9, 1/31 U [2/3,...

1. A function with a square root cannot have a domain that is the set of real numbers? 2. It is possible for an odd function to have the interval [0, () as its domain. 3. It is impossible for an even...

Suppose f has a real root r and Newtons method is used to approximate r with an initial approximation x 0 . The basin of attraction of r is the set of initial approximations that produce a sequence...

Let F be a subfield of a field E. a. Define an evaluation homomorphism 1 ,, n : F[x 1 , , X n ] E for i E stating the analog of Theorem 22.4. b. With E = F = (Q), compute -3,2 (x 1 2 x 2 3 + 3x...

F = E = Z 7 in Theorem 22.4. Compute for the indicated evaluation homomorphism. 4 (3x 106 + 5x 99 + 2x 53 ) Data from Theorem 22.4 Let F be a subfield of a field E. let a be any element of E, and let...

At temperatures between 775C (1048 K) and 1100C (1373 K), the activation energy and preexponential for the diffusion coefficient of Fe 2+ in FeO are 102,000 J/mol and 7.3 10 -8 m 2 /s, respectively....

Calculate the diameter of for the rod if the safety factor for point B is three (3). Assume material to be ductile with F = 600 N. Element A 150 mm 100 mm Rigid Element Yield Strength = 300 MPa...

10. Liberalism has turned our welfare system from a social safety net into a hammock. We hand out money with few questions asked. When welfare recipients are asked for some contribution to our...

Explain the following 1. Diffreence berween Turbine and Pump 2. Francis, Pelton, Kaplan Turbine 3. Reciprocating Pump and Centrifugal Pump.

The management of Sugar Daddy Cupcakes are analyzing two competing investment projects and must decide which one should be done immediately and which one to postpone for at least a year. The details...

Using an accident report that your research, analyzing the crew's communication. Be sure to include all crew members (including any outside agencies); do not focus on only certain crew positions. Was...

8:07 a webassign.net 1. [-/4 Points] DETAILS ROLFFM8 3.3.001. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Set up the constraints and objective function for the following linear programming problem. A...

answer the question clearly You are building a flight-control system for which a convincing safety case must be made. Would you assign the tasks of safety requirements engineering, test case...

1. Let x = day of observation and y = number of locusts per square meter during a locust infestation in a region of North Africa. Let x = day of observation and y = number of locusts per square meter...

pls show working where required according to question. Give full justications for answers to Qlv] and to all parts of Q2 except Q2(viii). For Q1(i], Q1(ii], Ql(iii) and Q2(viii) only the answer is...

pls solve this question correctly in 10 min i will give u like for sure (1) Let X have N(0, 1) distribution, call it P. Let Y = X + 2. Find the probability measure Q 80 that Y has N (0, 1)...

. (Generating Random Variables) Generating random variables with a desired probabil ity distribution is an important element of man},r engineering design applications. In this question, you will use...