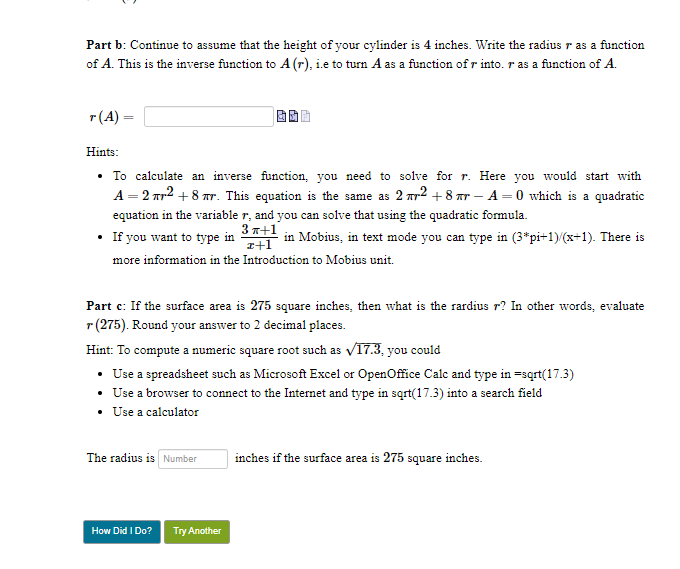
Remaining Time: Unlimited Module Two Discussion Question: Solve the problem below. For your initial post in Brightspace, copy the description of your cylinder in the box below and then enter your solution to all three parts (parts a, b, and c) of the problem. To copy the description of your cylinder, highlighting and using "copy" from here in Mobius and then using "paste" into Brightspace should work. Hint: This is similar to Question 63 in Section 5.7 of our textbook. We covered this section in "1- 4 Reading and Participation Activities: Inverses and Radical Functions" in Module One. You can check some of your answers to parts b and c to make sure that you are on the right track. The height of the cylinder is 4 inches. We'll be analyzing the surface area of a round cylinder - in other words the amount of material needed to "make a can". A cylinder (round can) has a circular base and a circular top with vertical sides in between. Let r be the radius of the top of the can and let h be the height. The surface area of the cylinder, A, is A =2mr- + 2wrh (it's two circles for the top and bottom plus a rolled up rectangle for the side) = radius Areas = 1 12 h = height Area = h(2xr) Circumference Part a: Assume that the height of your cylinder is 4 inches. Consider A as a function of r, so we can write that as A (r) = 2 ar- + 8 mr. What is the domain of A (r)? In other words, for which values of r is A (r) defined? Part b: Continue to assume that the height of your cylinder is 4 inches. Write the radius ~ as a function of A. This is the inverse function to A (r), i.e to turn A as a function of r into. r as a function of A. T (A) = Hints:Part b: Continue to assume that the height of your cylinder is 4 inches. Write the radius ~ as a function of A. This is the inverse function to A (r), i.e to turn A as a function of r into. r as a function of A. T (A) = Hints: . To calculate an inverse function, you need to solve for r. Here you would start with A =2 mr2+ 8 mr. This equation is the same as 2 my- + 8 ar - A=0 which is a quadratic equation in the variable r, and you can solve that using the quadratic formula. . If you want to type in 3 x+1 in Mobius, in text mode you can type in (3*pi+1)/(x+1). There is more information in the Introduction to Mobius unit. Part c: If the surface area is 275 square inches, then what is the rardius y? In other words, evaluate (275). Round your answer to 2 decimal places. Hint: To compute a numeric square root such as v17.3, you could . Use a spreadsheet such as Microsoft Excel or OpenOffice Calc and type in =sqrt(17.3) . Use a browser to connect to the Internet and type in sqrt(17.3) into a search field . Use a calculator The radius is Number inches if the surface area is 275 square inches. How Did I Do? Try AnotherAll: Answer is correct It gives cussect solution for part CO. May be way of writing is not correct 2IT 2 2 + 8TT 2 - A 20 quadratic in 2 arebo fc = 0 a = 21, b = 817, C = - A quadratic solution 8 2 b I / b 2 jac M = - SHT I J(8 12 2 4 X2TIX (-A )_-SPI VGUT12 +8 1 A as 870. , are neglect negative value 9 = 64172 + STTA - 872 ( GUTT 2 + 8 ITA ) 12 - 817 4 IT try worting this ( 6 4 71 2 + SITA ) ? # 2 4217 - 2 = 8 IT + A - 2 2 10 2 IT 7 ( s pi + A ) / Bapu ] - 2