Required using Maple.

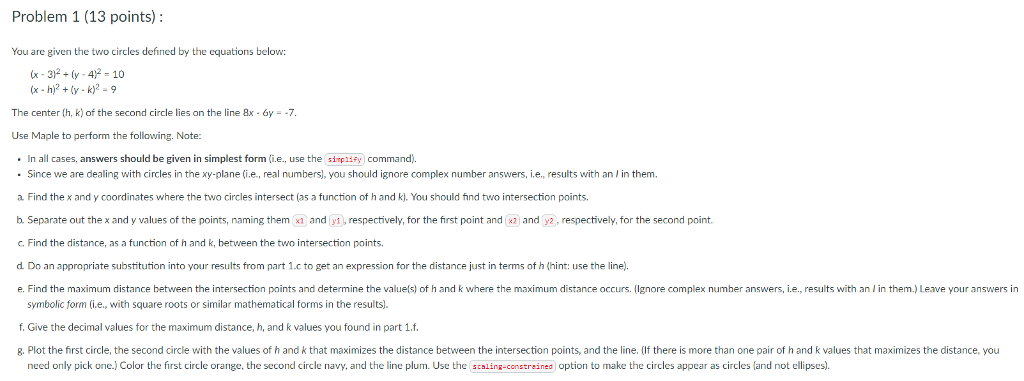
Problem 1 (13 points): You are given the two circles defined by the equations below: x-3P+(y-4-10 (x- hy-k)2 -9 The center (h, k) of the second circle lies on the line 8x 6y--7 Use Maple to perform the following. Note: In all cases, answers should be given in simplest form (i.e., use the simplify command) Since we are dealing with circles in the xy-plane (i.e., real numbers), you should ignore complex number answers, i.e, results with an in them. a. Find the x and y coordinates where the two circles intersect (as a function of h and k). You should find two intersection points. b. Separate out the x and y values of the points, naming them x andy), respectively, for the first point and(2 and 2, respectively, for the second point. c. Find the distance, as a function of h and k, between the two intersection points. d. Do an appropriate substitution into your results from part 1.c to get an expression for the distance just in terms of h (hint: use the line) e. Find the maximum distance between the intersection points and determine the valuels) of h and k where the maximum distance occurs. (Ignore complex number answers, i.e., results with an I in them.) Leave your answers in symbolic form(i.e., with square roots or similar mathematical forms in the results). f Give the decimal values for the maximum distance, h, and k values you found in part 1.f. 8. Plot the first circle, the second circle with the values of h and k that maximizes the distance between the intersection points, and the line. (If there is more than one pair of h and k values that maximizes the distance, you need only pick one. Color the first circle orange, the second circle navy, and the line plum. Use the scalin-constrained option to make the circles appear as circles (and not ellipses) Problem 1 (13 points): You are given the two circles defined by the equations below: x-3P+(y-4-10 (x- hy-k)2 -9 The center (h, k) of the second circle lies on the line 8x 6y--7 Use Maple to perform the following. Note: In all cases, answers should be given in simplest form (i.e., use the simplify command) Since we are dealing with circles in the xy-plane (i.e., real numbers), you should ignore complex number answers, i.e, results with an in them. a. Find the x and y coordinates where the two circles intersect (as a function of h and k). You should find two intersection points. b. Separate out the x and y values of the points, naming them x andy), respectively, for the first point and(2 and 2, respectively, for the second point. c. Find the distance, as a function of h and k, between the two intersection points. d. Do an appropriate substitution into your results from part 1.c to get an expression for the distance just in terms of h (hint: use the line) e. Find the maximum distance between the intersection points and determine the valuels) of h and k where the maximum distance occurs. (Ignore complex number answers, i.e., results with an I in them.) Leave your answers in symbolic form(i.e., with square roots or similar mathematical forms in the results). f Give the decimal values for the maximum distance, h, and k values you found in part 1.f. 8. Plot the first circle, the second circle with the values of h and k that maximizes the distance between the intersection points, and the line. (If there is more than one pair of h and k values that maximizes the distance, you need only pick one. Color the first circle orange, the second circle navy, and the line plum. Use the scalin-constrained option to make the circles appear as circles (and not ellipses)