resolve and explain

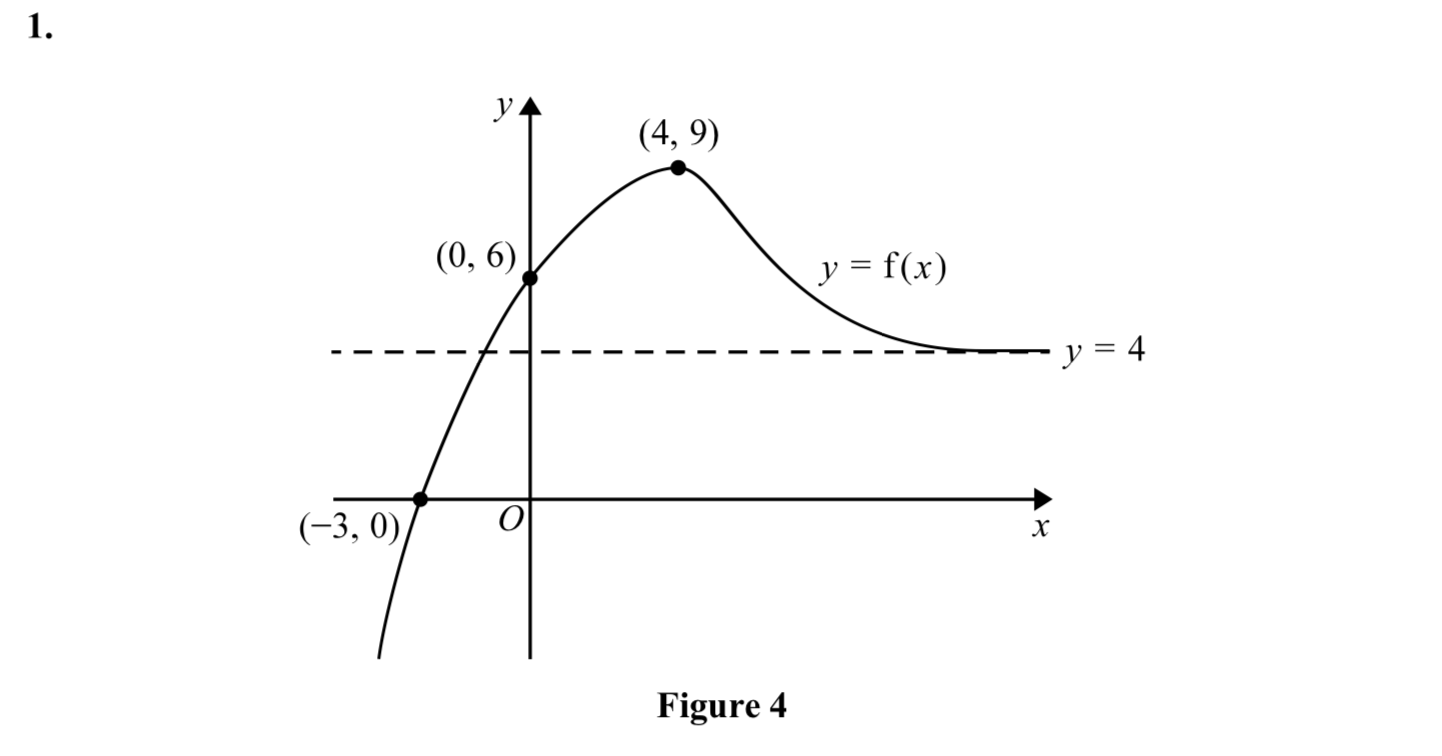
The curve C with equation y = f (x) is shown in Figure 4. The curve C 0 has a single turning point, a maximum at (4, 9) o crosses the coordinate axes at only two places, (3, 0) and (0, 6) O has a single asymptote with equation y = 4 as shown in Figure 4. (a) State the equation of the asymptote to the curve with equation y = f(-x). (1) l (b) State the coordinates of the turning point on the curve with equation y = f (EX). (1) Given that the line with equation y = k, where k is a constant, intersects C at exactly one point, (c) state the possible values for k. (2) The curve C is transformed to a new curve that passes through the origin. (d) (i) Given that the new curve has equation y = f (x) - a, state the value of the constant a. (ii) Write down an equation for another single transformation of C that also passes through the origin. (2) \f