Rigid$-$Body Kinematics Project

Instructions

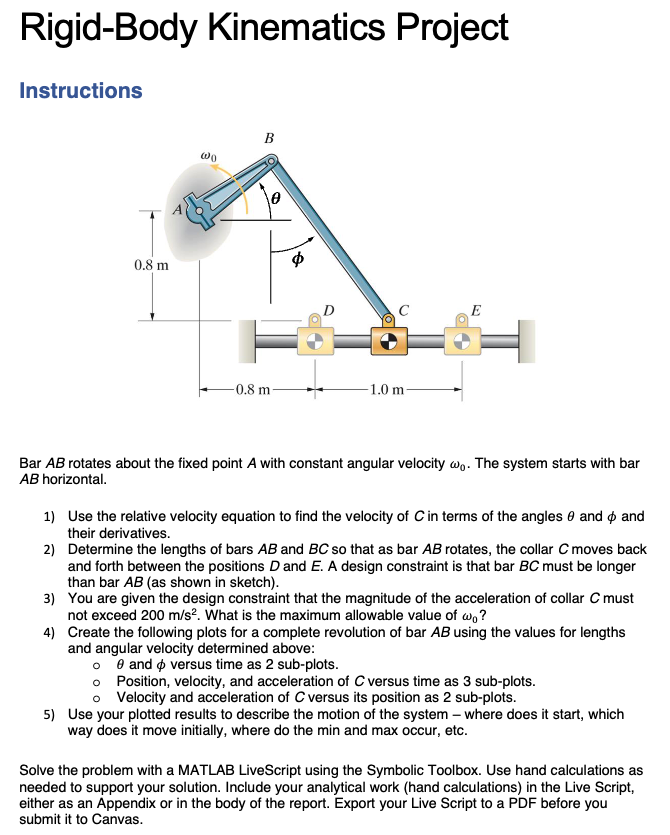
Bar $\backslash ($ A B $\backslash )$ rotates about the fixed point $\backslash ($ A $\backslash )$ with constant angular velocity $\backslash (\backslash$omega$\_\{0\}\backslash ).$ The system starts with bar $\backslash ($ A B $\backslash )$ horizontal.

$1)$ Use the relative velocity equation to find the velocity of $\backslash ($ C $\backslash )$ in terms of the angles $\backslash (\backslash$theta $\backslash )$ and $\backslash (\backslash$phi $\backslash )$ and their derivatives.

$2)$ Determine the lengths of bars $\backslash ($ A B $\backslash )$ and $\backslash ($ B C $\backslash )$ so that as bar $\backslash ($ A B $\backslash )$ rotates, the collar $\backslash ($ C $\backslash )$ moves back and forth between the positions $\backslash ($ D $\backslash )$ and $\backslash ($ E $\backslash ).$ A design constraint is that bar $\backslash ($ B C $\backslash )$ must be longer than bar $\backslash ($ A B $\backslash )($as shown in sketch$).$

$3)$ You are given the design constraint that the magnitude of the acceleration of collar $\backslash ($ C $\backslash )$ must not exceed $\backslash (200\backslash$mathrm$\{$~m$\}/\backslash$mathrm$\{$s$\}^\{2\}\backslash ).$ What is the maximum allowable value of $\backslash (\backslash$omega$\_\{0\}\backslash )?$

$4)$ Create the following plots for a complete revolution of bar $\backslash ($ A B $\backslash )$ using the values for lengths and angular velocity determined above:

$-\backslash (\backslash$theta $\backslash )$ and $\backslash (\backslash$phi $\backslash )$ versus time as $2$ sub$-$plots.

$-$ Position, velocity, and acceleration of $\backslash ($ C $\backslash )$ versus time as $3$ sub$-$plots.

$-$ Velocity and acceleration of $\backslash ($ C $\backslash )$ versus its position as $2$ sub$-$plots.

$5)$ Use your plotted results to describe the motion of the system $-$ where does it start, which way does it move initially, where do the min and max occur, etc.

Solve the problem with a MATLAB LiveScript using the Symbolic Toolbox. Use hand calculations as needed to support your solution. Include your analytical work $($hand calculations$)$ in the Live Script, either as an Appendix or in the body of the report. Export your Live Script to a PDF before you submit it to Canvas.