Ring theory

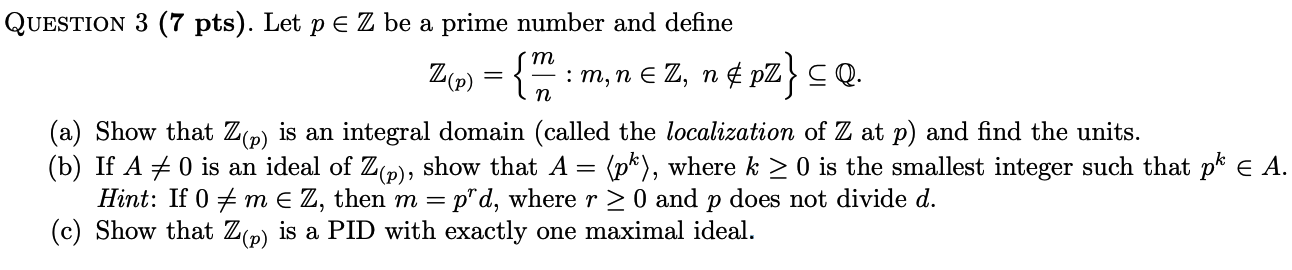
QUESTION 3 (7 pts). Let p E Z be a prime number and define Z ( P ) = 1m:m,nEZ, nepZ CQ. (a) Show that Z(p) is an integral domain (called the localization of Z at p) and find the units. (b) If A # 0 is an ideal of Z(p), show that A = (p*), where k 2 0 is the smallest integer such that p* E A. Hint: If 0 # m E Z, then m = p d, where r 2 0 and p does not divide d. (c) Show that Z(p) is a PID with exactly one maximal ideal