Question: RSA Cryptography 5. (10 pts) Consider the deterministic RSA, where the signature is computed using the private exponent and the modulus for the message m:

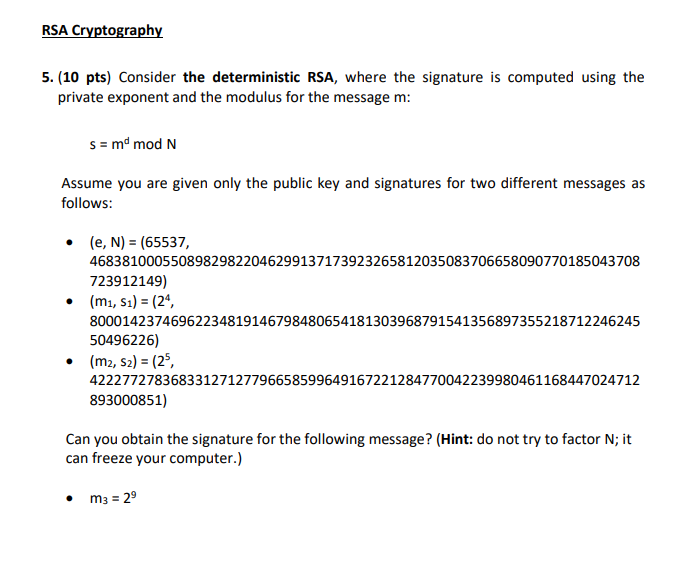
RSA Cryptography 5. (10 pts) Consider the deterministic RSA, where the

RSA Cryptography 5. (10 pts) Consider the deterministic RSA, where the signature is computed using the private exponent and the modulus for the message m: s = md mod N Assume you are given only the public key and signatures for two different messages as follows: . (e, N) = (65537, 46838100055089829822046299137173923265812035083706658090770185043708 723912149) (mi, S1) = (24, 80001423746962234819146798480654181303968791541356897355218712246245 50496226) (m2, 52) = (25, 42227727836833127127796658599649167221284770042239980461168447024712 893000851) Can you obtain the signature for the following message? (Hint: do not try to factor N; it can freeze your computer.) m3 = 29 RSA Cryptography 5. (10 pts) Consider the deterministic RSA, where the signature is computed using the private exponent and the modulus for the message m: s = md mod N Assume you are given only the public key and signatures for two different messages as follows: . (e, N) = (65537, 46838100055089829822046299137173923265812035083706658090770185043708 723912149) (mi, S1) = (24, 80001423746962234819146798480654181303968791541356897355218712246245 50496226) (m2, 52) = (25, 42227727836833127127796658599649167221284770042239980461168447024712 893000851) Can you obtain the signature for the following message? (Hint: do not try to factor N; it can freeze your computer.) m3 = 29

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

How to attempt this? RSA signatures, V7f (10 marks) Consider the following variant of the RSA signature scheme. Signature generation. To sign a message m E {0, 1}*, Alice does: (a) Compute h = H(m),...

1) We can design a MAC function that generates MAC tags as follows: Select one: a. All the options b. Use AES or 3DES in CFB mode c. Use a hash function along with a secret shared key d. Use AES or...

Applied Cryptography Any language like --------------------------------------------- rsa.data Problem 1 part (b) =================== RSA public key (e,N) and plaintext m is given by e := 3 N :=...

PROBLEM 1 GCD EXTENDED-EUCLID(a,b) where a b 1 if a mod b = 0 return (0,1) 2 (x,y) + EXTENDED-EUCLID(b, a mod b) 3 return (y,x y(a/b])) Use the extended Euclid algorithm presented in class to compute...

PROBLEM 3 Textbook RSA is insecure Consider the textbook RSA signature scheme with the public key and private keys pk = e, sk = d, and die = 1 mod (n) for an RSA modulus n = pq and: 1. Signsk(m):...

Please solve c and d only RSA and digital signatures. Recall that in the RSA public-key cryptosystem, each user has a public key P = (N, e) and a secret key d. In a digital signature scheme, there...

Help me please. This is all about math in digital communication cryptography math. I am not sure with RSA cryptography and the conceptual questions so i only got 13/14. Would u help me identify my...

Problem 1 part (b) =================== RSA public key (e,N) and plaintext m is given by e := 3 N :=...

What is finance? Explain how this field affects the life of everyone and of every organization.

Obtain an expression for the frequency of radiation emitted when a hydrogen atom de- excites from level n to level (n-1). For large n, show that this frequency equals the classical frequency of...

Which of the following best describes the reason for establishing a stretch IRA? A ) To extend the period of tax - deferred earnings beyond the original owner s lifetime B ) To allow the owner to...

Seved Help 14 Wisconsin Snowmobile Corp. is considering a switch to level production Cost efficiencies would occur under level production, and aftertax costs would decline by $31,500, but inventory...

What would be the shared Data Elements between Position Control and Salary Grade Tables in providing cost input to Budgets for vacant positions?

What is the purpose of the Salary Structure Table?

What is the scope and use of a Job Family Table?