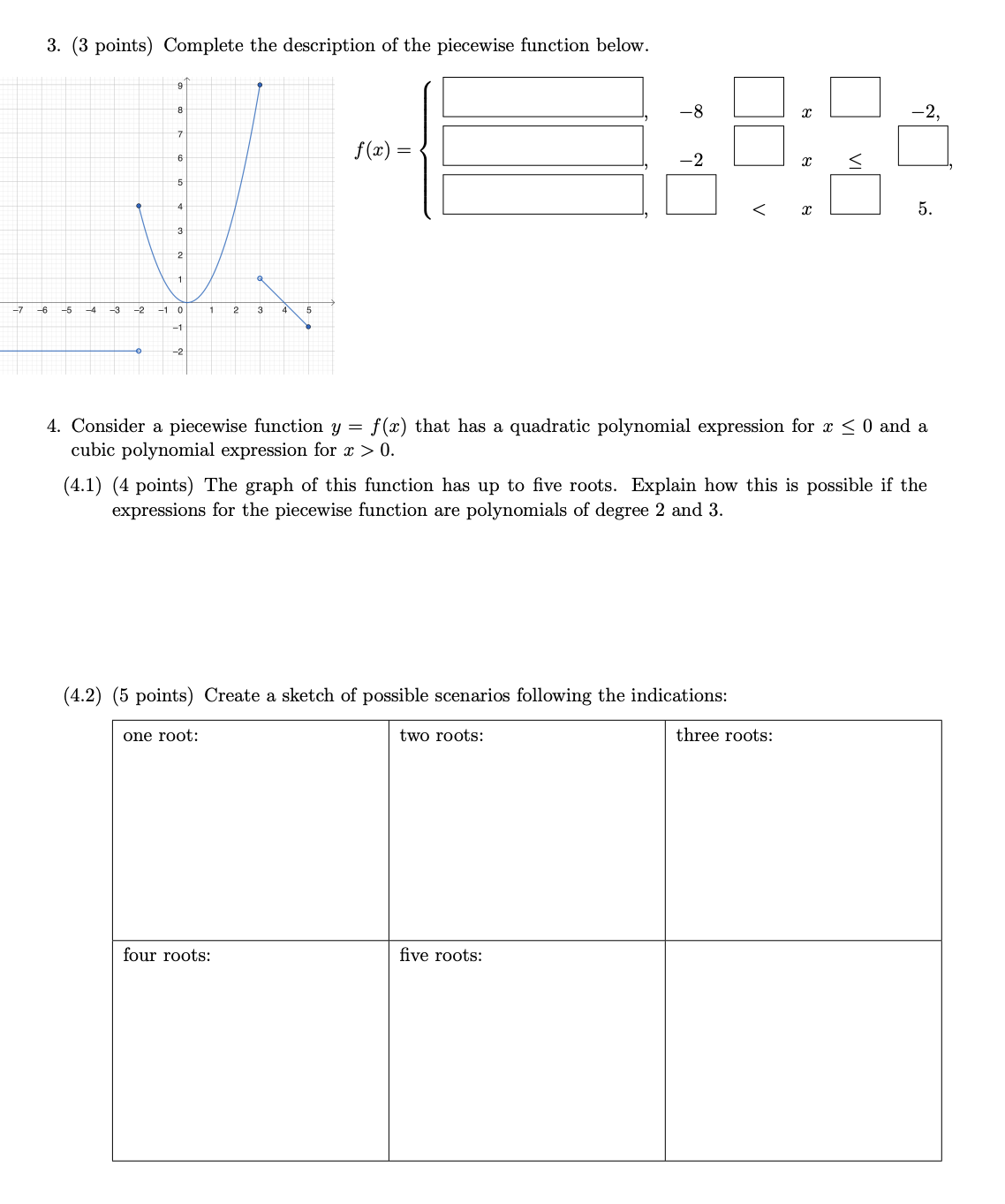
Rules/Suggestions: Write with a dark pencil, so that your work is visible. You are graded on your work, not just answers. Even if you do calculations in your head or on scratch paper, show work if space is provided. Write the final answer in the box. 1. We can write a polynomial f(z) in standard form: f(z) = z* + 62* 22z + 15 or in factored form f(x) = (z 13z + 3)(z + 5). (1.1) (3 points) Which form is easier to use to find the zero? Explain why it is easier to use? (1.2) (3 points) Which form is easier to find the y-intercept. Explain why it is easier to use. 2. (3 points) The function f is a degree 4 function. It has exactly three zeros and they are -2, 4 and 5. This is not enough information to make a general sketch of f.! There are SIX possible different general sketches of f. Sketch them. 1A general sketch shows the location of the zeroes, whether the function is positive or negative between them and then end behavior. It does not show the precise values of the function except at the zeros. 3. (3 points) Complete the description of the piecewise function below. ! 4. Consider a piecewise function y = f(z) that has a quadratic polynomial expression for z 0. (4.1) (4 points) The graph of this function has up to five roots. Explain how this is possible if the expressions for the piecewise function are polynomials of degree 2 and 3. (4.2) (5 points) Create a sketch of possible scenarios following the indications: one root: two roots: three roots: four roots: five roots: 5. Identify the transformations necessary to create a graph of f(z) = 5(z 2)2 + 3. Provide an explanation to every answer. (5.1) (3 points) Stretch: yes O no Q. (5.2) (3 points) Reflection: yes O no O. (5.3) (3 points) Vertical translation: yes O no Q. (5.4) (3 points) Horizontal translation: yes O) no (). (5.5) (3 points) Sketch a graph of the function. It must include the vertex with the corresponding coordinates. Pl 6. You are given the composition g o f(z) = 2z + 17. (6.1) (3 points) Give an example of f(z) and g(z) that produce the desired composition of the begin- ning. (6.2) (3 points) Give an example of f and g, with the condition that the function f must have an 23 in its definition. (6.3) (3 points) Explain why in the parts 1 and 2 there are different possibilities. 7. (5 points) Let h(x) be a function such that h o h(z) = 2z + 17. Suppose that h(z) = az + b, find the values of a and b. 8. (0 points) Special Word! There's nothing to fill in for this question and it's not worth points this week...but after the quiz is graded, look at the feedback in Gradescope to this question to find the special word for next week. 9. (0 points) If there are any issues with formatting or if the quiz is submitted late (Wednesday or Thursday), you will see feedback here