Runge kutta method 4th order-RK4.this is a matlab question (please put the code).also explain the Runge kutta method if possible.

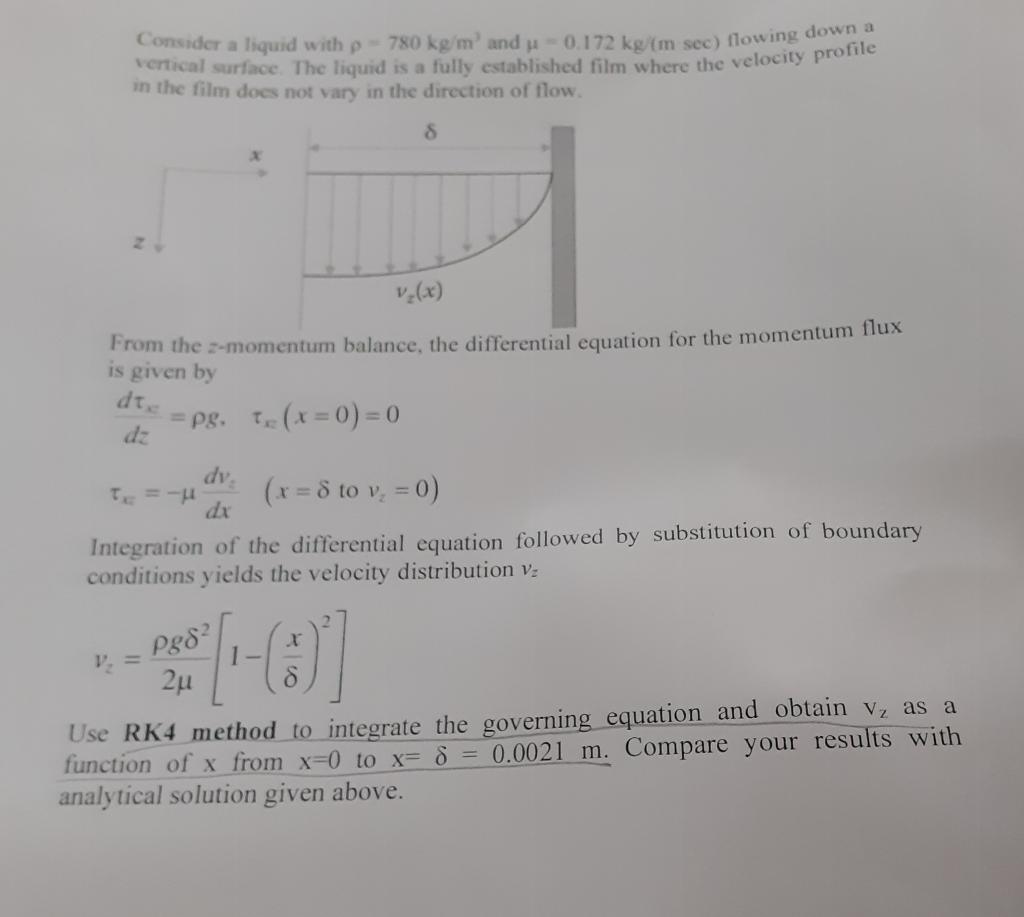
Consider a liquid with =780kg/m3 and =0.172kg(m sec) flowing down a vertical surface. The liquid is a fully established film where the velocity profile in the film does not vary in the direction of flow. From the z-momentum balance, the differential equation for the momentum flux is given by dzdx=g,x(x=0)=0xE=dxdvz(x=tovz=0) Integration of the differential equation followed by substitution of boundary conditions yields the velocity distribution vz vz=2g2[1(x)2] Use RK4 method to integrate the governing equation and obtain vz as a function of x from x=0 to x==0.0021m. Compare your results with nalytical solution given above. Consider a liquid with =780kg/m3 and =0.172kg(m sec) flowing down a vertical surface. The liquid is a fully established film where the velocity profile in the film does not vary in the direction of flow. From the z-momentum balance, the differential equation for the momentum flux is given by dzdx=g,x(x=0)=0xE=dxdvz(x=tovz=0) Integration of the differential equation followed by substitution of boundary conditions yields the velocity distribution vz vz=2g2[1(x)2] Use RK4 method to integrate the governing equation and obtain vz as a function of x from x=0 to x==0.0021m. Compare your results with nalytical solution given above