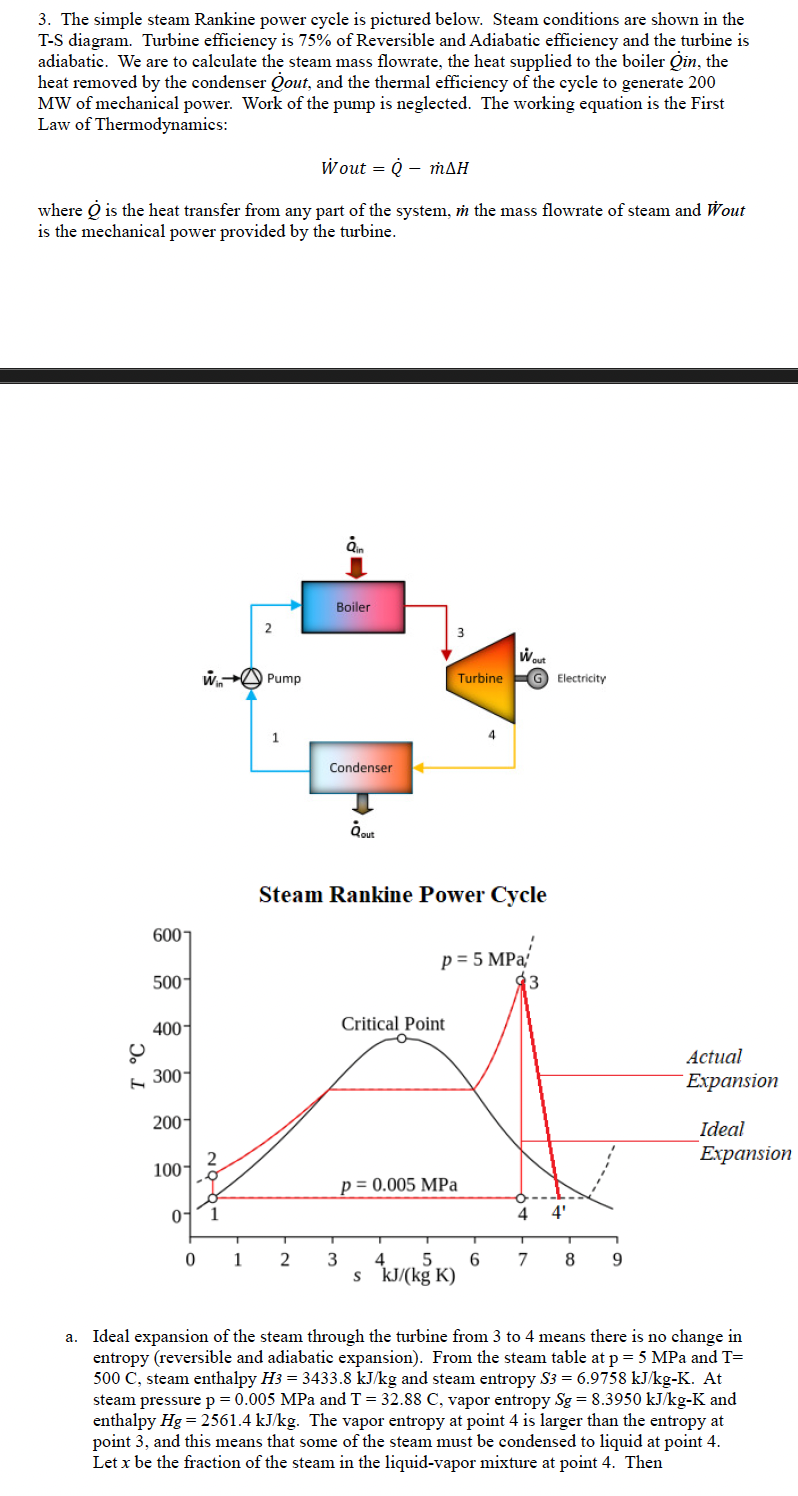
$S_4=S_3=(1-x)S_f+x{S}_g$

where $Sf=0\mathrm{.}5763k\frac{J}{k}g-K$ and $Sg=8\mathrm{.}3950k\frac{J}{k}g-K$ are the entropy values of the

saturated liquid and vapor steam, respectively at $p=0\mathrm{.}005$MPa. The equation for $S4$can

be solved for steam fraction $x.$ At $0\mathrm{.}005$ MPa $,$ enthalpy of the liquid $Hf=137\mathrm{.}79k\frac{J}{k}g$

and vapor $Hg=2561\mathrm{.}4k\frac{J}{k}g,$ and knowing $x$ we can calculate

$H_4=(1-x)H_f+x{H}_g$

Then $(H4-H3)=(H)s=-2728k\frac{J}{k}g$ is the enthalpy change at constant entropy. The

actual change in entropy $H=(H{4}^{\text{'}}-H3)=(H)s=-2046k\frac{J}{k}g$ and $$ is the given

turbine efficiency.

Use the above information and the given $W^{}$ out for the mechanical power of turbine

calculate the mass flowrate $m^{}$ of the steam from the First Law of Thermodynamics.

$[$Answer: $m^{}=97\mathrm{.}75k\frac{g}{s}.]$

b$.$ Heat $Q^{}in$ is added from point $2$ to point $3$ in the diagram. If the pump is adiabatic and

reversible the entropy at point $1$ is the same as the entropy at point $2.$ At point $1$ the

entropy of the saturated liquid $Sf=0\mathrm{.}4763k\frac{J}{k}g-K$ and enthalpy $Hf=137\mathrm{.}79k\frac{J}{k}g.$ At

point $2$ pressure $p=5$MPa and at the same entropy as point $1$ the enthalpy $H2=150$

$k\frac{J}{k}g.$ Then from the mass flowrate $m^{}$ calculate the heat added in the boiler:

$Q^{}in=m^{}(H_3-H_2)$

$[$Answer: Qin ${?}^{(}())=321\mathrm{.}0MW.]$

c$.$ Heat is removed from the condenser from points $4^{\text{'}}$ to point $1.$ There is an entropy

increase from point $4$ to point $4\text{'}$ because the turbine expansion is less than isentropic$.$

The enthalpy $H{4}^{\text{'}}\text{'}$ can be calculated from $H$ in part a$.$ Then calculate

Qout ${?}^{(}())=m^{}(H_{4^{\text{'}}}-H_2)$

$[$Answer: Qout ${?}^{(}())=135\mathrm{.}7MW.]$

d$.$ Calculate the cycle efficiency $=$ power out$/$heat in$.[$Answer: $62\mathrm{.}3\%.]$adiabatic$.$ We are to calculate the steam mass flowrate, the heat supplied to the boiler $Q^{}in,$ the

heat removed by the condenser $Q^{}$ out, and the thermal efficiency of the cycle to generate $200$

MW of mechanical power. Work of the pump is neglected. The working equation is the First

Law of Thermodynamics:

$W^{}$ out $=Q^{}-m^{}H$

where $Q^{}$ is the heat transfer from any part of the system, $m^{}$ the mass flowrate of steam and $W^{}$ out

is the mechanical power provided by the turbine.

Steam Rankine Power Cycle

a$.$ Ideal expansion of the steam through the turbine from $3$ to $4$ means there is no change in

entropy $($reversible and adiabatic expansion$).$ From the steam table at $p=5$MPa and $T=$

$500$ C $,$ steam enthalpy $H3=3433\mathrm{.}8k\frac{J}{k}g$ and steam entropy $S3=6\mathrm{.}9758k\frac{J}{k}g-K.$ At

steam pressure $p=0\mathrm{.}005$MPa and $T=32\mathrm{.}88C,$ vapor entropy $Sg=8\mathrm{.}3950k\frac{J}{k}g-K$ and

enthalpy $Hg=2561\mathrm{.}4k\frac{J}{k}g.$ The vapor entropy at point $4$ is larger than the entropy at

point $3,$ and this means that some of the steam must be condensed to liquid at point $4.$

Let $x$ be the fraction of the steam in the liquid$-$vapor mixture at point $4.$ Then