sample	x1	1 x2	x3	x1	2 x2	x3	x1	3 x2	x3
1	0.28	1.31	-6.2	0.011	1.03	-0.21	1.36	2.17	0.14
2	0.07	0.58	-0.78	1.27	1.28	0.08	1.41	1.45	-0.38
3	1.54	2.01	-1.63	0.13	3.12	0.16	1.22	0.99	0.69
4	-0.44	1.18	-4.32	-0.21	1.23	-0.11	2.46	2.19	1.31
5	-0.81	0.21	5.73	-2.18	1.39	-0.19	0.68	0.79	0.87
6	1.52	3.16	2.77	0.34	1.96	-0.16	2.51	3.22	1.35
7	2.20	2.42	-0.19	-1.38	0.94	0.45	0.60	2.44	0.92
8	0.91	1.94	6.21	-0.12	0.82	0.17	0.64	0.13	0.97
9	0.65	1.93	4.38	-1.44	2.31	0.14	0.85	0.58	0.99
10	-0.26	0.82	-0.96	0.26	1.94	0.08	0.66	0.51	0.88

Section 6.3

2. Create a 3-1-1 sigmoidal network with bias to be trained to classifypatterns from ₁ and ₂ in the table above. Use stochastic backpropagation to (Algorithm 1) with learning rate = 0.1 and sigmoid as described in Eq. 33 in Sect. 6.8.2.

(a) Initialize all weights randomlyin the range 1 w +1. Plot a learning curve the training error as a function of epoch. (b) Now repeat (a) but with weights initialized to be the same throughout each level. In particular, let all input-to-hidden weights be initialized with w_ji = 0.5 and all hidden-to-output weights with w_kj = 0.5. (c) Explain the source of the differences between your learning curves (cf. Problem 12).

Attachments:

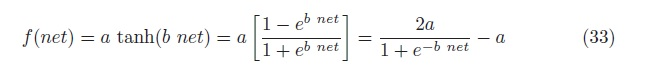
f(net) = a tanh(b net) = a [1+eb net1+ 1- eb net - e net 2 e-b net (33)