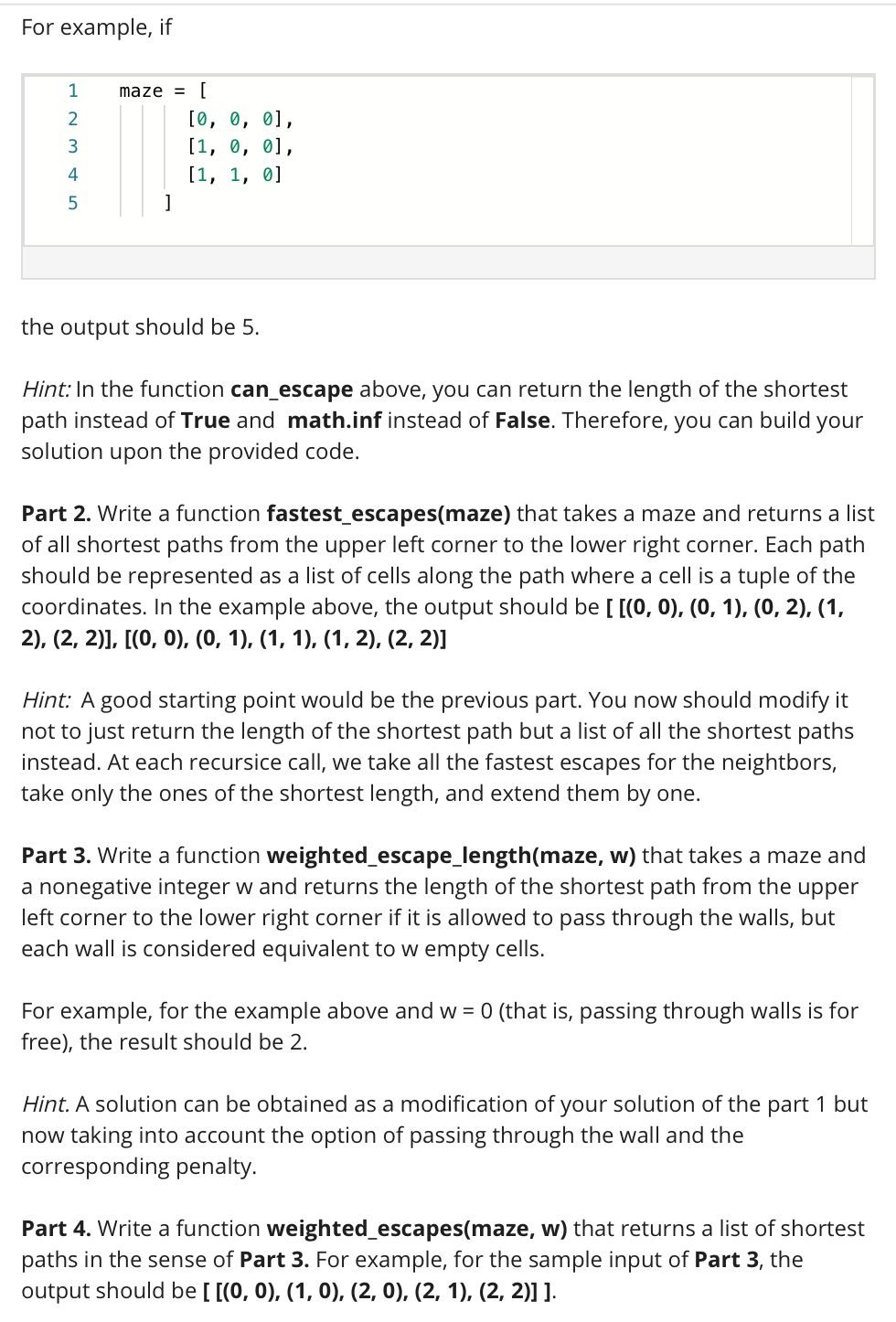
Question: Sample/Example: import math def fastest_escape_length(maze, i=0, j=0): pass def fastest_escapes(maze, i=0, j=0): pass def weighted_escape_length(maze, w, i=0, j=0): pass def weighted_escapes(maze, w, i=0, j=0): pass

Sample/Example:
import math
def fastest_escape_length(maze, i=0, j=0):
pass
def fastest_escapes(maze, i=0, j=0):
pass
def weighted_escape_length(maze, w, i=0, j=0):
pass
def weighted_escapes(maze, w, i=0, j=0):
pass
# some test code
if __name__ == "__main__":
test_a = [
[0, 0, 0],
[1, 1, 0],
[1, 1, 0]
]
# should print 5
print(fastest_escape_length(test_a))
# should print 2
print(weighted_escape_length(test_a, 0))
test_b = [
[0, 0, 0],
[1, 1, 1],
[0, 0, 0]
]
# should print inf
print(fastest_escape_length(test_b))
# should print 5
print(weighted_escape_length(test_b, 1))
# should print 6
print(weighted_escape_length(test_b, 2))
# should print [[(0, 0), (0, 1), (0, 2), (1, 2), (2, 2)]]
print(fastest_escapes(test_a))
# should print []
print(fastest_escapes(test_b))
# should print [5, 5, 5, 5, 5, 5]
print(list(map(len, fastest_escapes([[0 for _ in range(3)] for _ in range(3)]))))
# should print [[(0, 0), (1, 0), (1, 1), (1, 2), (2, 2)]]
print(weighted_escapes(test_b, 0))
# should print [[(0, 0), (1, 0), (2, 0), (2, 1), (2, 2)], [(0, 0), (0, 1), (1, 1), (2, 1), (2, 2)], [(0, 0), (0, 1), (0, 2), (1, 2), (2, 2)]]
# the order of the paths within the list might be different
print(weighted_escapes(test_b, 2))
Input: a maze defined by a 2-d array maze where maze[i][j] is equal to 0 if the j-th cell on the i-th row is empty and 1 if there is a wall there. It is guaranteed that the upper left and lower right cells are empty. Output: True if there exists a path from the upper left cell to the lower right cell passing through empty cells only. False otherwise. A path can go from a cell to a cell that shares a side with it. Below is a python implementation of the algorithm we have designed. 1 2 3 4 5 6 7 8 def can_escape (maze, i=0, j=0): # (i, j) is the starting position # maze [x] [y] = 0 (x, y) cell is empty # maze[x][y] = 1 (x, y) cell contains a wall n = len(maze) m = len(maze [0]). if i == n - 1 and j == m - 1: return True maze[i][j] = 1 result = False for a, b in [(i - 1, j), (i, j - 1), (i + 1, j), (i, j + 1)]: if 0 (x, y) cell is empty # maze[x][y] = 1 (x, y) cell contains a wall n = len(maze) m = len(maze [0]). if i == n - 1 and j == m - 1: return True maze[i][j] = 1 result = False for a, b in [(i - 1, j), (i, j - 1), (i + 1, j), (i, j + 1)]: if 0
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


