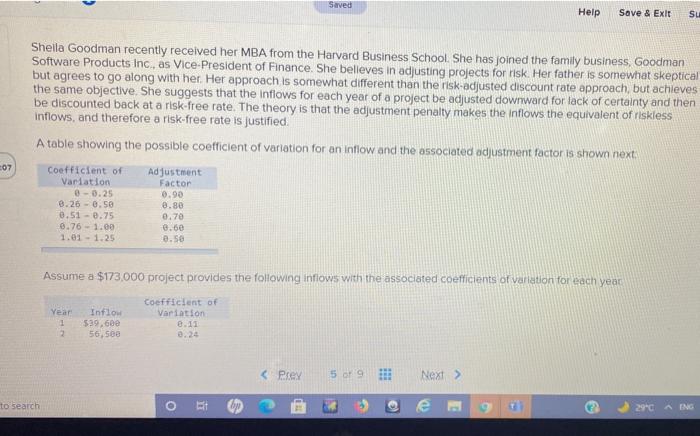
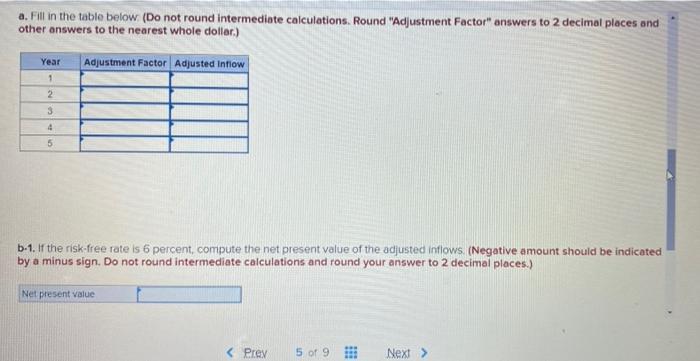
Saved Help Save & Exit su Sheila Goodman recently received her MBA from the Harvard Business School. She has joined the family business Goodman Software Products Inc., as Vice-President of Finance. She believes in adjusting projects for risk. Her father is somewhat skeptical but agrees to go along with her. Her approach is somewhat different than the risk-adjusted discount rate approach, but achieves the same objective. She suggests that the inflows for each year of a project be adjusted downward for lack of certainty and then be discounted back at a risk-free rate. The theory is that the adjustment penalty makes the inflows the equivalent of riskless inflows, and therefore a risk-free rate is justified. A table showing the possible coefficient of variation for an inflow and the associated adjustment factor is shown next Coefficient of Adjustment Factor 0 - 0.25 8.26 -0.50 07 Variation 0.51 -0.75 0.76 - 1.00 1.0 - 1.25 0.90 8.80 0.70 8.60 2.50 Assume a $173.000 project provides the following inflows with the associated coefficients of variation for each year Year 1 2 Inflow $39.600 56,50e Coefficient of Variation 0.11 2.24 Prey 5 9 Next > to search O 29CAIN a. Fill in the table below (Do not round Intermediate calculations. Round "Adjustment Factor" answers to 2 decimal places and other answers to the nearest whole dollar.) Year Adjustment Factor Adjusted Inflow 1 2 3 4 5 b-1. If the risk-free rate is 6 percent, compute the net present value of the adjusted inflows (Negative amount should be indicated by a minus sign. Do not round intermediate calculations and round your answer to 2 decimal places.) Net present value Saved Help Save & Exit su Sheila Goodman recently received her MBA from the Harvard Business School. She has joined the family business Goodman Software Products Inc., as Vice-President of Finance. She believes in adjusting projects for risk. Her father is somewhat skeptical but agrees to go along with her. Her approach is somewhat different than the risk-adjusted discount rate approach, but achieves the same objective. She suggests that the inflows for each year of a project be adjusted downward for lack of certainty and then be discounted back at a risk-free rate. The theory is that the adjustment penalty makes the inflows the equivalent of riskless inflows, and therefore a risk-free rate is justified. A table showing the possible coefficient of variation for an inflow and the associated adjustment factor is shown next Coefficient of Adjustment Factor 0 - 0.25 8.26 -0.50 07 Variation 0.51 -0.75 0.76 - 1.00 1.0 - 1.25 0.90 8.80 0.70 8.60 2.50 Assume a $173.000 project provides the following inflows with the associated coefficients of variation for each year Year 1 2 Inflow $39.600 56,50e Coefficient of Variation 0.11 2.24 Prey 5 9 Next > to search O 29CAIN a. Fill in the table below (Do not round Intermediate calculations. Round "Adjustment Factor" answers to 2 decimal places and other answers to the nearest whole dollar.) Year Adjustment Factor Adjusted Inflow 1 2 3 4 5 b-1. If the risk-free rate is 6 percent, compute the net present value of the adjusted inflows (Negative amount should be indicated by a minus sign. Do not round intermediate calculations and round your answer to 2 decimal places.) Net present value