Script box to be filled please !

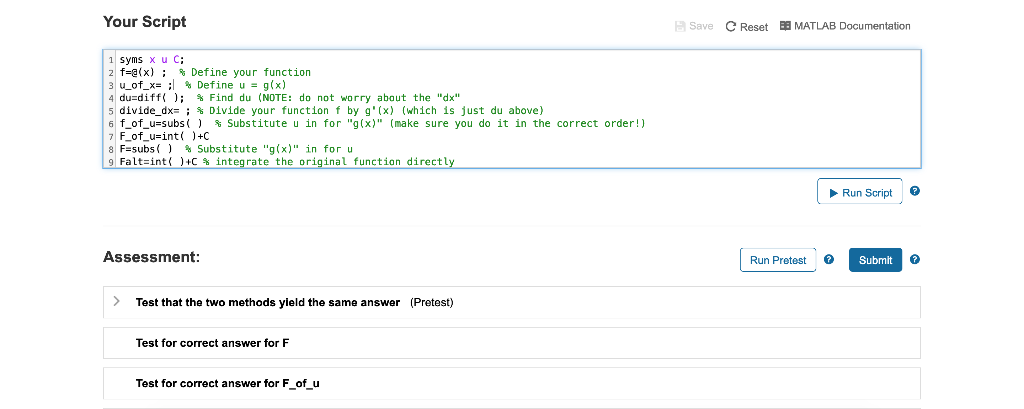
Understanding Substitution (Indefinite Integral) Recall the Chain Rule for derivatives: ( Mg(x)))'=r(g(x))g(x) Substitution is nothing more than rewriting this rule in Integral form by letting u gx) My Solutions> f (g()) g'(x) da -J f'(u) du =f(u) + C f(g(x))C Note that, if u=g( ), then du-g'(x)" dx using differential notation, so d_du/g'(x) Use this idea and the strategy outlined in the Solution Template to evaluate 3 Then use int lo evaluate the integral directly to compare answers. Rele help symbolic subs.html to this pagg to a , with making our substitutions f needed t pww.matm rs.com Your Script Save C Reset MATLAB Documentation 1 syms x uC; 2 f-g(x) ; % Define your function 4 dusd ift( ); Find du (NOTE: do not wo rry about the "dx" 5 divide-dxz ; % Divide your function f byg"(x) (which is just du above) f-of-ussubs ( ) % Substitute u in for "g(x)" (make sure you do it in the correct order!) 7F_of u-int )+C F-subsSubstitute "g(x)" in for u 9. Faltaint( )hC % integrate the original function directly Run Script Assessment Run Pretest Submit Test that the two methods yleld the same answer (Pretest) Test for correct answer for F Test for correct answer for F_of_u