Section 10.4 Reading Assignment: Comparison Tests

Answer Only Exercise 1, 2, and 3 by using a screenshot provided Calculus Pearson textbook. Make sure you read these three questions very carefully and see on what it is asking for and what is really about. Please be very careful with this assignment.

References: Thomas' Calculus: Early Transcendentals | Calculus | Calculus | Mathematics | Store | Pearson+

Feedback: #1: Reread the exercise statement here carefully and thoroughly. This is about the corollary found in the exercise reading. The c value here is very specific. (0/2) #2: This should involve the details of this example. (0/2) #3: (0/2).

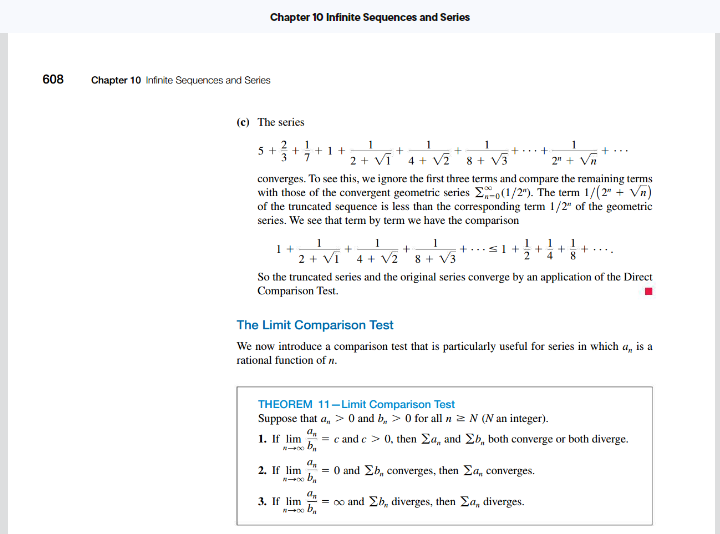
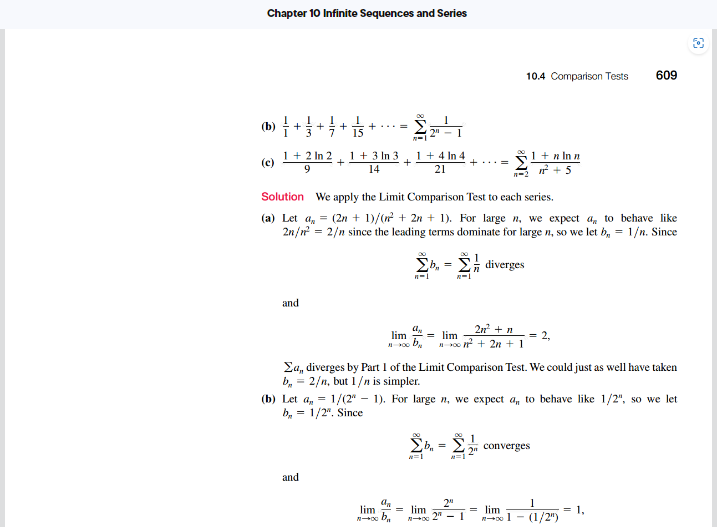
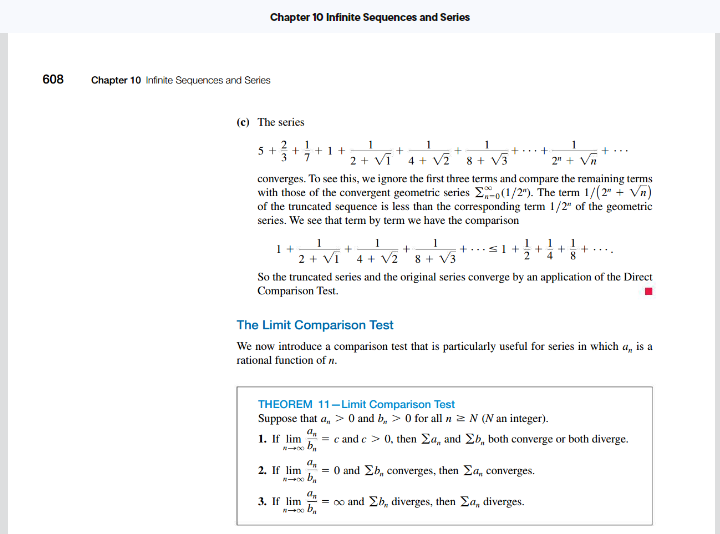
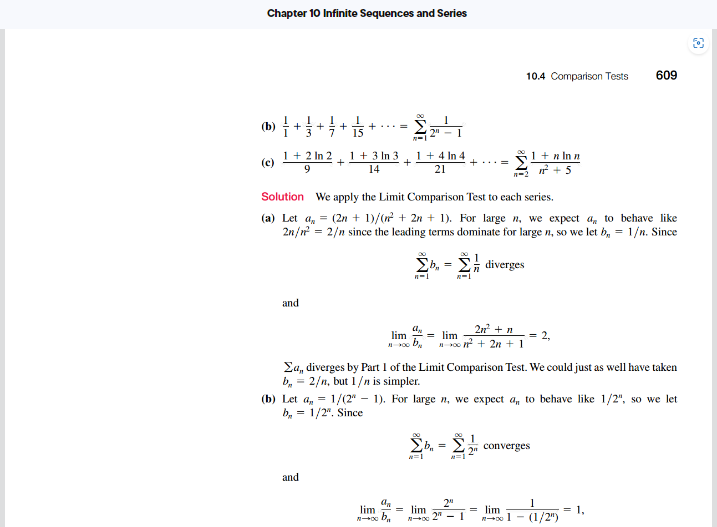
Section 10.4 Reading Assignment: Comparison Tests Instructions. Read through this assignment and complete the three exercises below by reading the appropriate passages of the textbook. We will be skipping the Direct Comparison Test. It seems like most students don't have much experience with inequalities and will often state one without justification. Even worse, students will often use false inequalities. To avoid these troubles all together, I think it's better to have a class rule that we ban the direct comparison test completely. In addition to skipping the direct comparison test, I think it's best to consider a version of the limit comparison test that uses asymptotic equality (see the Section 7.4 assignments for details). This specializes the situation more, but based on that material it also means we can find what series to use in the comparison easily. Exercise 1. Read Statement 1 of Theorem 11 - Limit Comparison Test (boxed on p. 608). Consider the following corollary: If an ~bn as n - co, then the series En=1 an and En=1 bn either both converge or both diverge. Explain how this corollary is a special case of Statement 1 of Theorem 11. In particular, explain what the value of c is in this corollary. In my opinion, it's best to avoid using Statement 2 or 3 of the limit comparison test. In contrast to the direct comparison test, you can use them if you want, but the asymmetric nature of these statements makes them easy to misapply.Exercise 2. Read Example 2, part (a) (p. 608 -609). Restate the statement "we expect a, to behave like.." as a statement involving asymptotic equality (~). Exercise 3. Read Example 2, part (b) (p. 608 -609). Restate the statements "we expect a, to behave like." as a statement involving asymptotic equality (~). Notice that to apply the limit comparison test, we need an easier series to compare with. This version of the limit comparison test means that we can use asymptotic equality to find a good candidate, which will often be a p-series, whose convergence we know all about. 1 A corollary is a result that follows from the result of a theorem. In this situation, we are specializing the limit comparison test to use asymptotic equality.Chapter 10 Infinite Sequences and Series 608 Chapter 10 Infinite Sequences and Series (c) The series + ... 2+ V1 4+ V2 8 + V3 2" + Vn converges. To see this, we ignore the first three terms and compare the remaining terms with those of the convergent geometric series _, (1/2"). The term 1/(2" + Va) of the truncated sequence is less than the corresponding term 1/2" of the geometric series. We see that term by term we have the comparison 1 + 2+ VI 4+ 12 8+ V3 So the truncated series and the original series converge by an application of the Direct Comparison Test. The Limit Comparison Test We now introduce a comparison test that is particularly useful for series in which a,, is a rational function of n. THEOREM 11-Limit Comparison Test Suppose that a, > 0 and b, > 0 for all n 2 N (N an integer). 1. If lim b " = cand c > 0. then Za, and 2b, both converge or both diverge. 2. If lim " = 0 and Eb, converges, then Za, converges. 3. If lim " = oo and 2b, diverges, then Ed,, diverges.Proof We will prove Part 1. Parts 2 and 3 are left as Exercises 57a and h. Since c/2 > 0, there exists an integer / such that Limit definition with whenever n >N. e - c/2, L - e, and a. replaced by a./be Thus, for n > N. 2 2 If Eb,, converges, then E(3c/2)b, converges and Za, converges by the Direct Comparison Test. If 2b,, diverges, then E(c/2)6,, diverges and Za,, diverges by the Direct Comparison Test. EXAMPLE 2 Which of the following series converge, and which diverge? (a) + + 7 + 9 20 + 1 2n + 1 + iME 16 25 - = (n + 1)2 in' + 2n + 1Chapter 10 Infinite Sequences and Series 10.4 Comparison Tests 609 +4 + + ...=27- (b) + 3+ 7+ 15 (e) 1 + 2 In 2 1+313 9 + 1 + 4 In 4 14 21 1 + 5 Solution We apply the Limit Comparison Test to each series. (a) Let a, = (2n + 1)/(wr + 2n + 1). For large n, we expect a, to behave like 27/m = 2 since the leading terms dominate for large n, so we let by = 1. Since Eh, = ME diverges and lim " = lim 2n' + n = 2, a poor + 2n + 1 In, diverges by Part 1 of the Limit Comparison Test. We could just as well have taken be = 2, but 1 is simpler. (b) Let a, = 1/(2" - 1). For large a, we expect a,, to behave like 1/2", so we let b = 1/2". Since 1 Con converges and On = lim 2" lim = lim 1-+03 1 - (1/2") 1,Ia, converges by Part 1 of the Limit Comparison Test. (c) Leta, = (1 + n In n)/(n' + 5). For large n, we expect a, to behave like (n In n)) = (Inn), which is greater than 1 for a 2 3, so we let b, = 1. Since 18 diverges and lim = 00, 7+ 5 Ed, diverges by Part 3 of the Limit Comparison Test. EXAMPLE 3 Does In a converge? Solution Because In a grows more slowly than of for any positive constant c (Section 10.1, Exercise 115), we can compare the series to a convergent p-series. To get the p-series, we see that In n n1/4