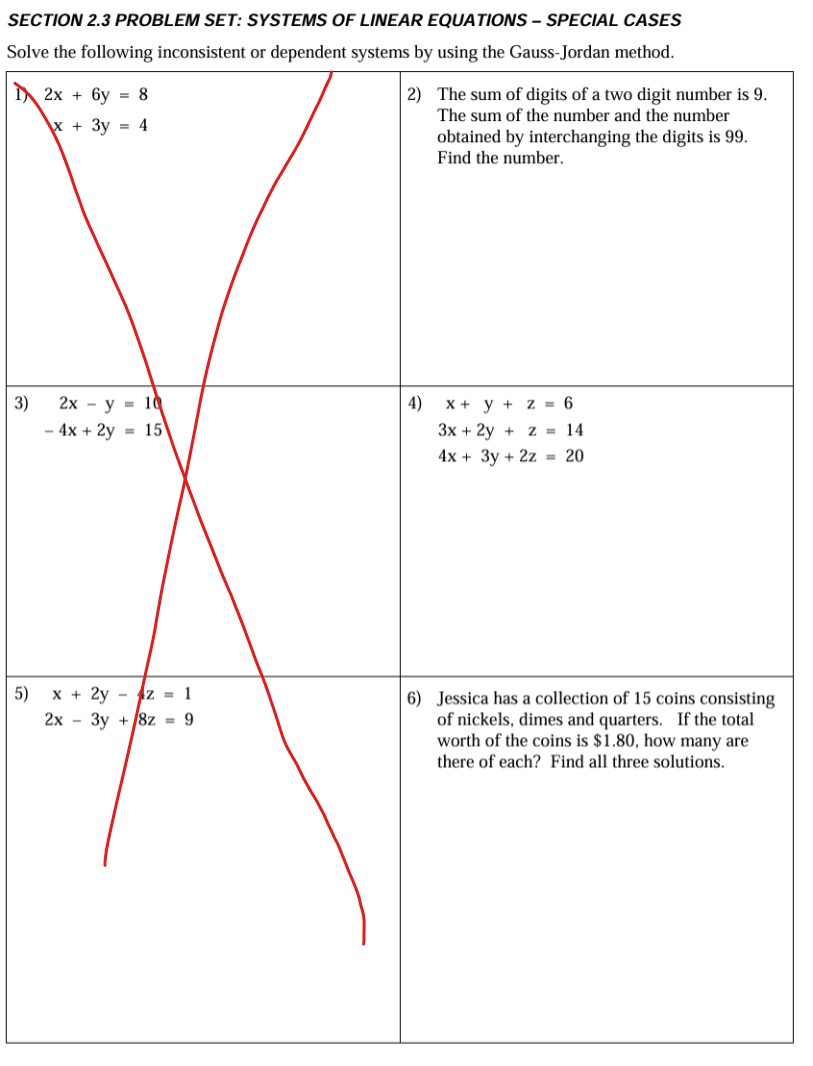
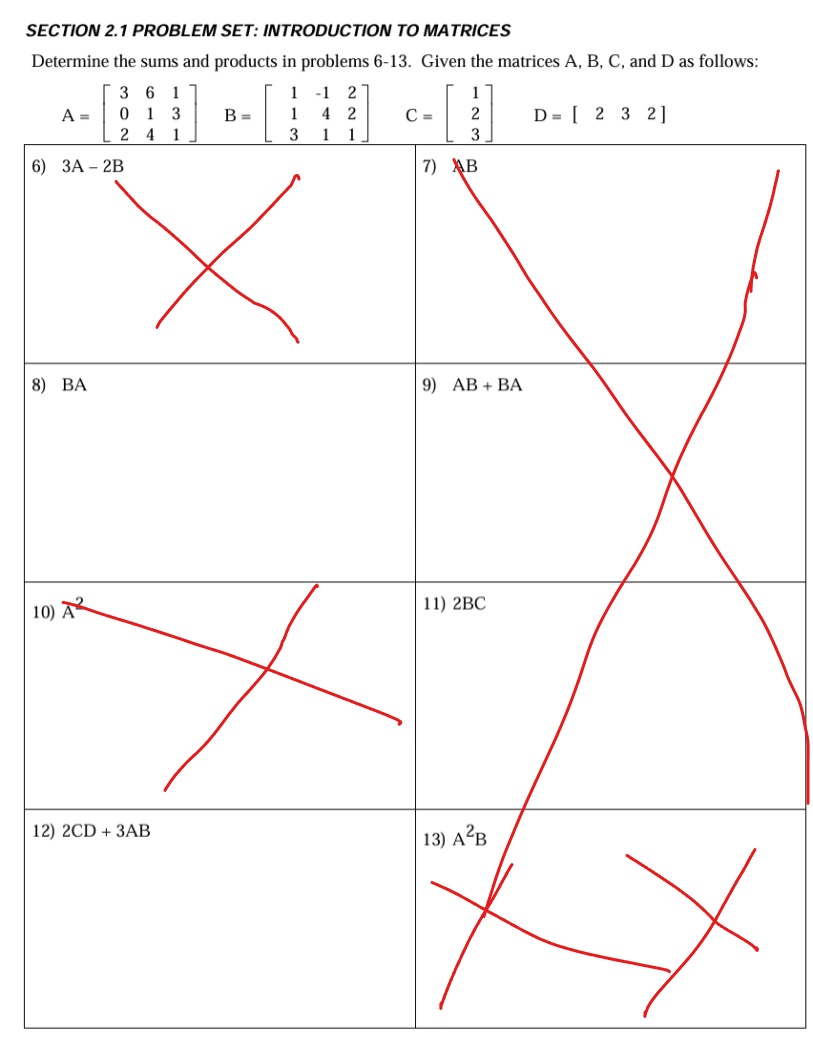
SECTION 2.3 PROBLEM SET: SYSTEMS OF LINEAR EQUATIONS - SPECIAL CASES Solve the following inconsistent or dependent systems by using the Gauss-Jordan method. 2) The sum of digits of a two digit number is 9. The sum of the number and the number obtained by interchanging the digits is 99. Find the number, 4) X+ Yy + z 3x+2y + 2 4x + 3y + 22 6) Jessica has a collection of 15 coins consisting of nickels, dimes and quarters. If the total worth of the coins is $1.80, how many are there of each? Find all three solutions. SECTION 2.3 PROBLEM SET: SYSTEMS OF LINEAR EQUATIONS - SPECIAL CASES Solve the following inconsistent or dependent systems by using the Gauss-Jordan method. 7) A company is analyzing sales reports for 8) x + y +2z = 0 three products: products X, Y, Z. One report Shows that a combined total of 20/600 of x + 2y + Z = 0 items X, Y, and Z were sold. Another report 2x + 3y + 3z = 0 shows that the sum of the number of item Z sold and twice the number of itzm X sold equals 10,000. Also item X has 5,000 more items sold than item Y Are these reports consistent? 9) Find three solutions to the following system 10) x + 2y = 5 of equations. 2x + 4y = k x + 2y + 2 = 12 For what values of k does this system of equations have a) No solution? b) Infinitely many solutions? 11) x + 3y - Z = 5 12) Why is it not possible for a linear system to have exactly two solutions? Explain geometrically.SECTION 2.1 PROBLEM SET: INTRODUCTION TO MATRICES Determine the sums and products in problems 6-13. Given the matrices A, B, C, and D as follows: 3 6 2 A B= D = [ 2 3 2 ] 3 6) 3A - 2B 7) AB X 8) BA 9) AB + BA 10) A 11) 2BC 12) 2CD + 3AB 13) A B