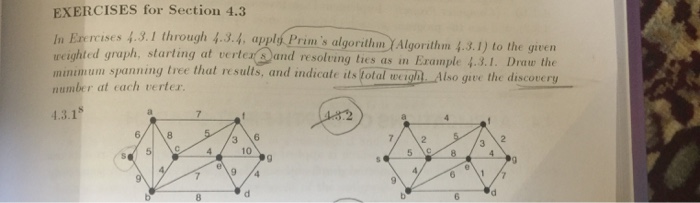
Section 4 3 Minimum Spanning Trees and Shortest Paths DEFINITION: Let S be the current set of froutier edges. The function Prim-nextEdge is defined as follows: Prim-netEdye (G, S) selects and returns as its value the fron ier edge with smallest edge-weight. If there is more than one such edge, then Prim- nert Edge(G, S) selects the one determined by the default priority Algorithm 4.3.1: Prim's Minimum Spanning Tree | Input: a weighted connected graph G and starting vertex r. Outpul: a minimum spanning tree T Initialize tree T as vertex. Initialize S as the set of proper edges incident on v. while S Let e = Prim-nezt Edge(G,S). Let w be the non-tree endpoint of edge e Add edge e and vertex u to tree T. update Frontier(G, S) Return tree T Example 4.3.1: Figure 4.3.1 shows the minimum spanning tree produced by Prim's algorithm for the input graph shown, starting at vertex v. The function nert Edge uses lexicographic order: of the names of the non-tree endpoints of frontier edges as a first. tie-breaker and of the tree-endpoints as a second tie-breaker. The discovery numbers appear in parentheses. 0) hin 9(3) a(2) b(4) 9 (6) Figure 4.3.1 Minimum spanning tree produced by Primi's algorithm. The correctness of Prim's algorithm is an immediate consequence of the next propo- sition. Proposition 4.3.1. Let Th be the Prim tree after k iterations of Prim's algorithm on a connected graph G, for 0SksIVal-1. Then T is a subtree of a minimum spanning tree of G. T, ithe trivial tree consisting