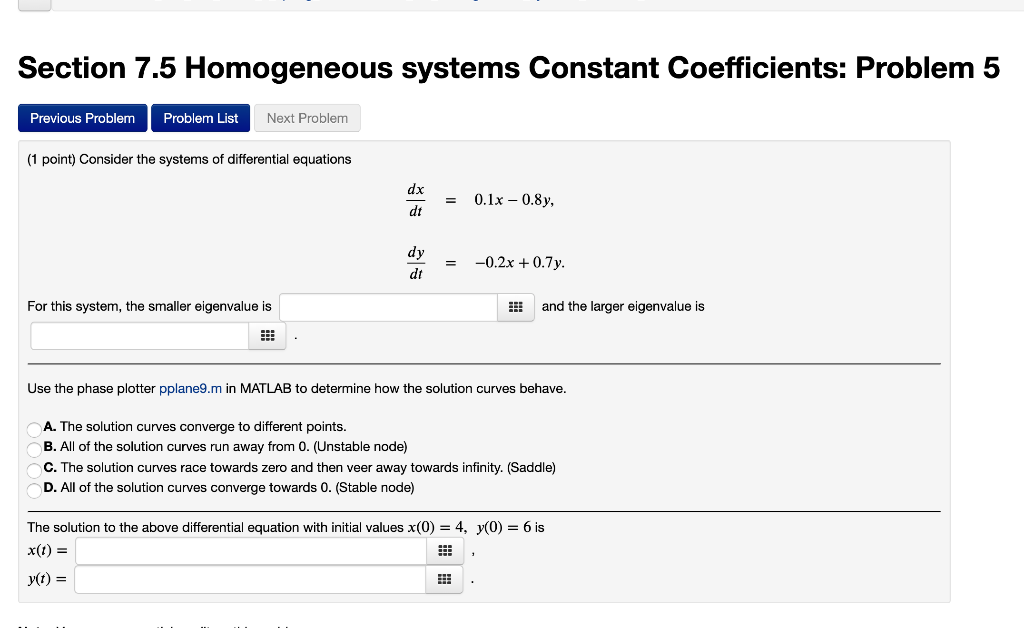
Section 7.5 Homogeneous systems Constant Coefficients: Problem 5 Previous Problem Problem List Next Problem (1 point) Consider the systems of differential equations = 0.18 0.8y, = -0.2x + 0.7y. For this system, the smaller eigenvalue is !!! and the larger eigenvalue is Use the phase plotter pplane9.m in MATLAB to determine how the solution curves behave. A. The solution curves converge to different points. B. All of the solution curves run away from 0. (Unstable node) C. The solution curves race towards zero and then veer away towards infinity. (Saddle) D. All of the solution curves converge towards 0. (Stable node) The solution to the above differential equation with initial values x(0) = 4, y(0) = 6 is x(1) = yt) =