See the following image for the linreg.py :

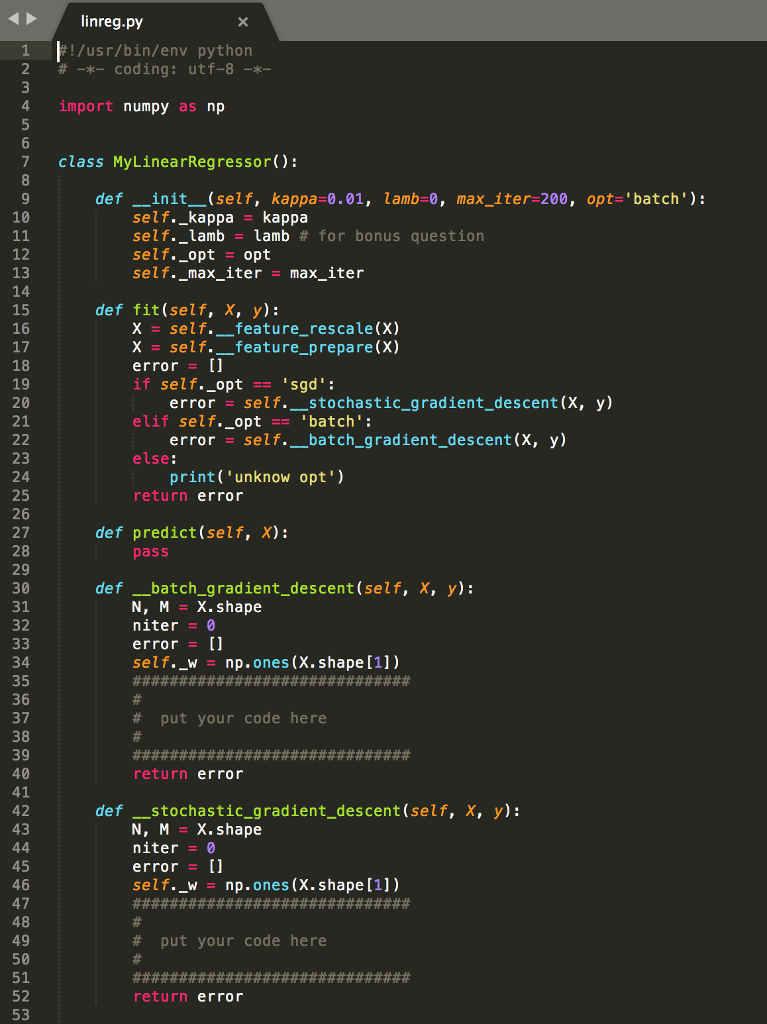
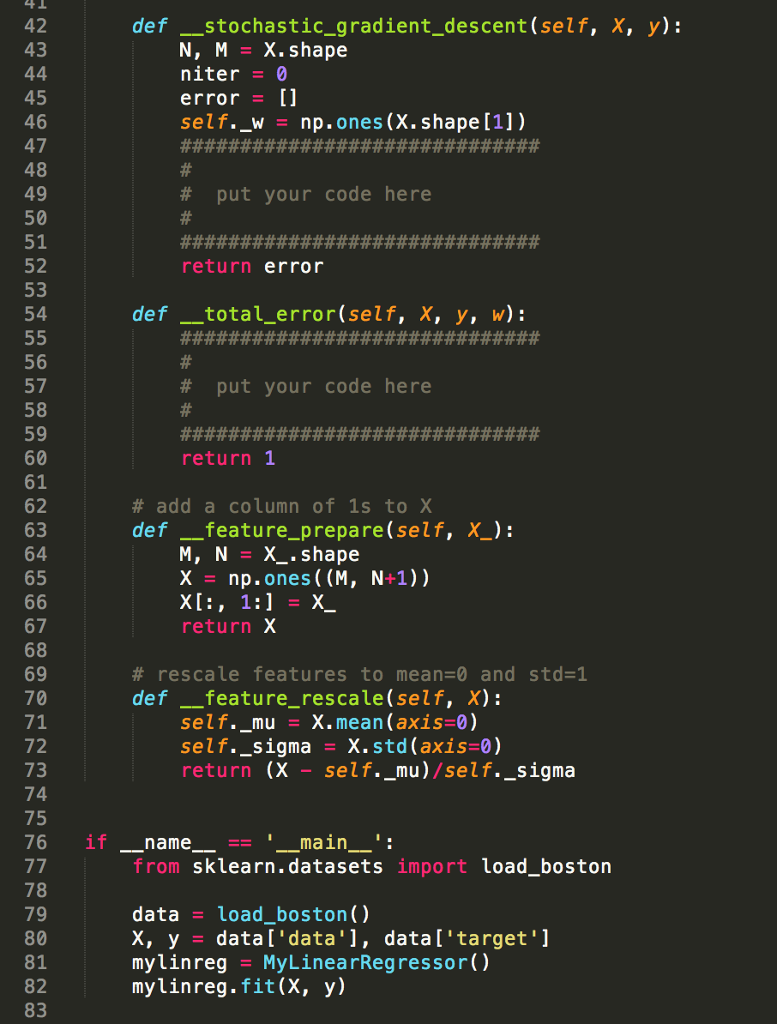
2. Gradient Descent: Linear Regression (SENG 474: 30 points, CSC578D: 40 points. SEng 474; CSc 587D: 5 Bonus points) In this part of the assignment we will implement a linear regression model, using the Boston houses dataset. We will implement two techniques for minimizing the cost function: batch gradient descent, and stochastic gradient descent. You are provided with a skeleton python program linreg.py and you have to implement the missing parts First let's recall some theory and mathematical notation We express our dataset as a matrix X E Rn*m where each row is a training sample and each column represents a feature, and a vector y Rn of target values. In order to make the following notation easier, we defined a training sample as vector as [Lx1,x2-..,xm]. Basically we add a column of ones to X. The purpose of linear regression is to estimate the vector of parameters w- [Wo, w1,... , wm] such that the hyper-plane a w7 fits, in an optimal way, our training samples. Once we have obtained w we can predict the value of testing sample, a,test, simply by plugging it into the equation y atest . w We estimate w by minimizing a cost function over the entire dataset, which is defined as follows we apply gradient descent techniques to find the parameters vector w that minimizes the cost function E(w). This is achieved by an iterative algorithm that starts with ain initial guess for w and repeatedly performs the update E(u) j= 0,1, where k is the learning rate parameter. In this question you are asked to implement some gradient descent techniques. We are going to set a maximum number of iteration, max_iter in the code, and analyze what happens to the cost function at each iteration by plotting the error function at each teration 2. Gradient Descent: Linear Regression (SENG 474: 30 points, CSC578D: 40 points. SEng 474; CSc 587D: 5 Bonus points) In this part of the assignment we will implement a linear regression model, using the Boston houses dataset. We will implement two techniques for minimizing the cost function: batch gradient descent, and stochastic gradient descent. You are provided with a skeleton python program linreg.py and you have to implement the missing parts First let's recall some theory and mathematical notation We express our dataset as a matrix X E Rn*m where each row is a training sample and each column represents a feature, and a vector y Rn of target values. In order to make the following notation easier, we defined a training sample as vector as [Lx1,x2-..,xm]. Basically we add a column of ones to X. The purpose of linear regression is to estimate the vector of parameters w- [Wo, w1,... , wm] such that the hyper-plane a w7 fits, in an optimal way, our training samples. Once we have obtained w we can predict the value of testing sample, a,test, simply by plugging it into the equation y atest . w We estimate w by minimizing a cost function over the entire dataset, which is defined as follows we apply gradient descent techniques to find the parameters vector w that minimizes the cost function E(w). This is achieved by an iterative algorithm that starts with ain initial guess for w and repeatedly performs the update E(u) j= 0,1, where k is the learning rate parameter. In this question you are asked to implement some gradient descent techniques. We are going to set a maximum number of iteration, max_iter in the code, and analyze what happens to the cost function at each iteration by plotting the error function at each teration