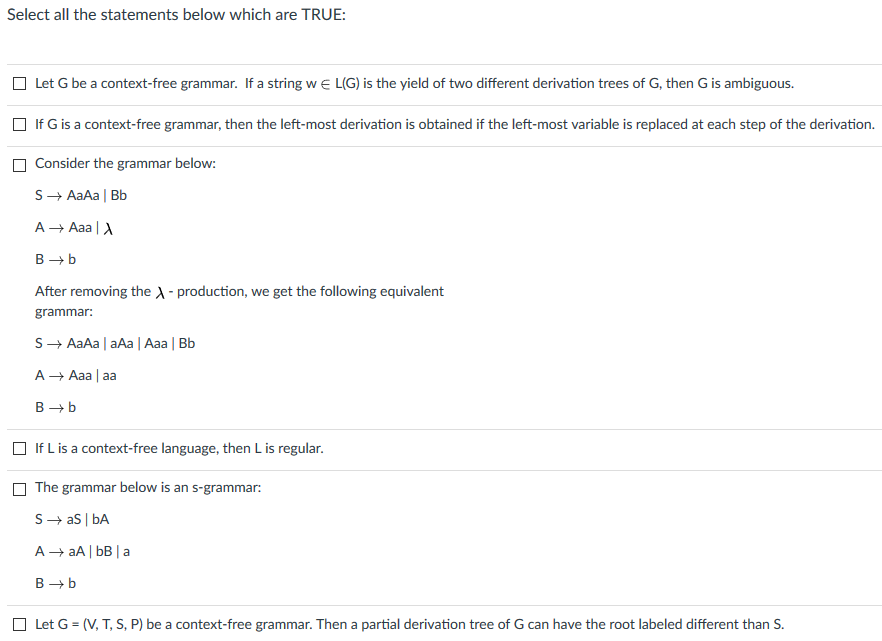
Select all the statements below which are TRUE: Let G be a context-free grammar. If a string w elementof L(G) is the yield of two different derivation trees of G, then G is ambiguous. If G is a context-free grammar, then the left-most derivation is obtained if the left-most variable is replaced at each step of the derivation. Consider the grammar below: S rightarrow AaAa | Bb A rightarrow Aaa | lambda B rightarrow b After removing the lambda - production, we get the following equivalent grammar: S rightarrow AaAa | aAa | Aaa | Bb A rightarrow Aaa | aa B rightarrow b If L is a context-free language, then L is regular. The grammar below is an s-grammar: S rightarrow aS | bA A rightarrow aA | bB | a B rightarrow b Let G = (V, T, S, P) be a context-free grammar. Then a partial derivation tree of G can have the root labeled different than S