Select have: O(1), O(|V|), O(|E|), O(|V| + |E|)

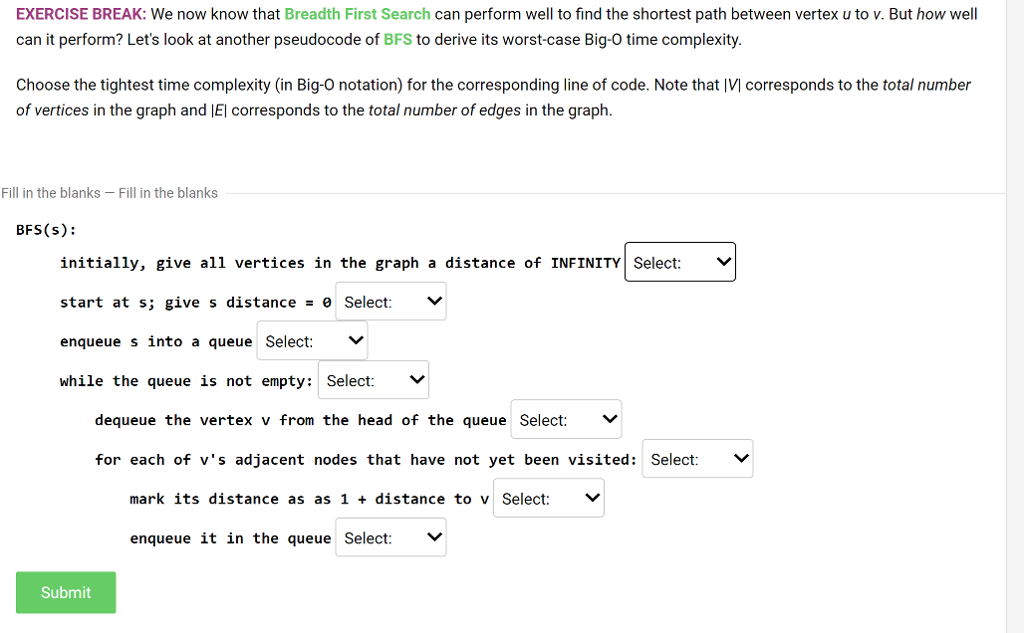
EXERCISE BREAK: We now know that Breadth First Search can perform well to find the shortest path between vertex u to v. But how well can it perform? Let's look at another pseudocode of BFS to derive its worst-case Big-O time complexity Choose the tightest time complexity (in Big-O notation) for the corresponding line of code. Note that IVI corresponds to the total number of vertices in the graph and IEl corresponds to the total number of edges in the graph. Fill in the blanks-Fill in the blanks BFS (s): initially, give all vertices in the graph a distance of INFINITY Select: v start at s; give s distance e Select: enqueue s into a queue Select while the queue is not empty: Select dequeue the vertex v from the head of the queue Select:Y for each of v's adjacent nodes that have not yet been visited: Select mark its distance as as 1 + distance to v Select enqueue it in the queue Select: Submit