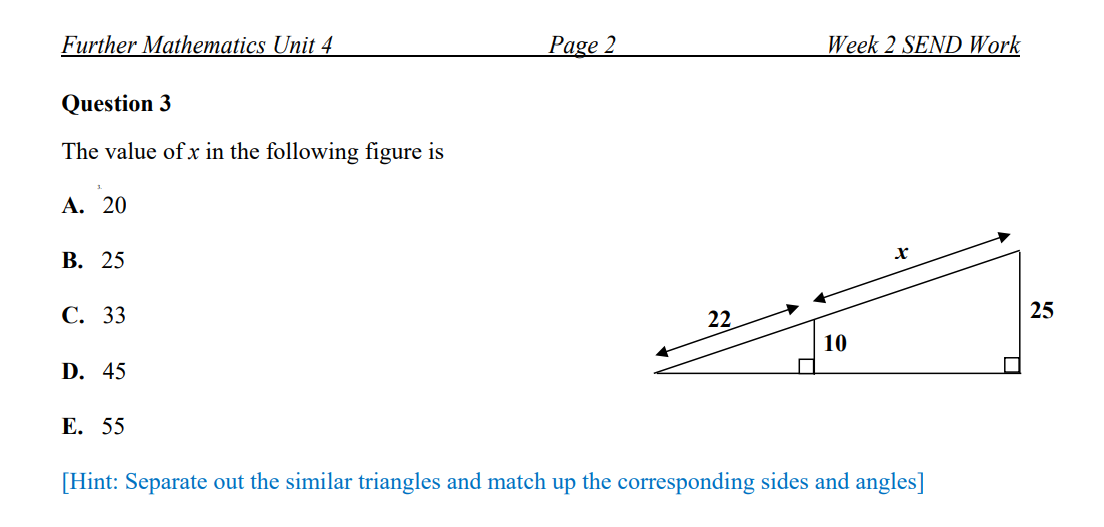
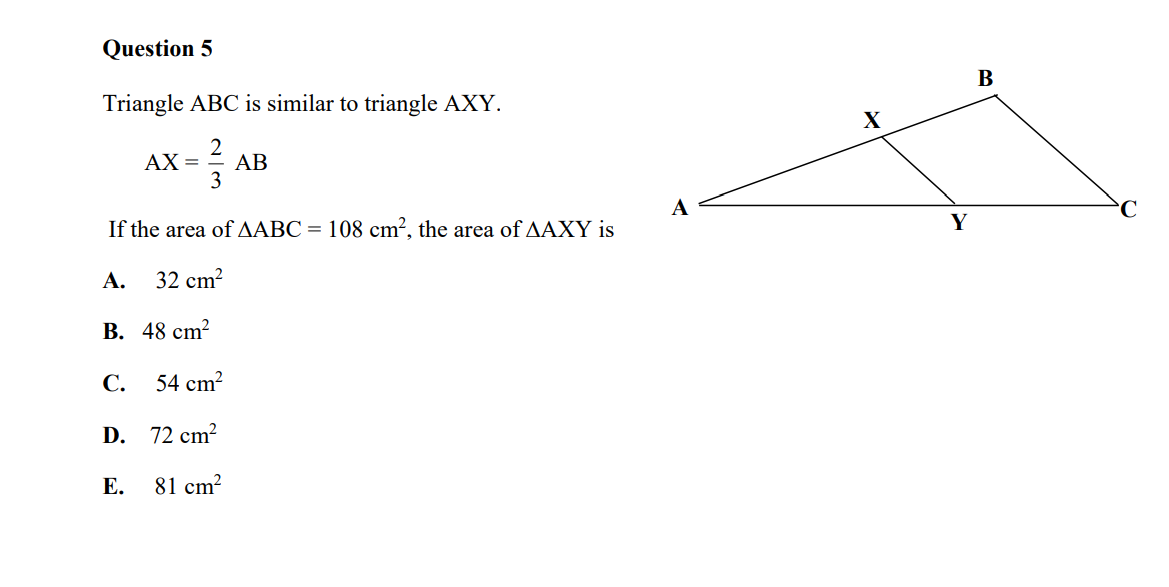
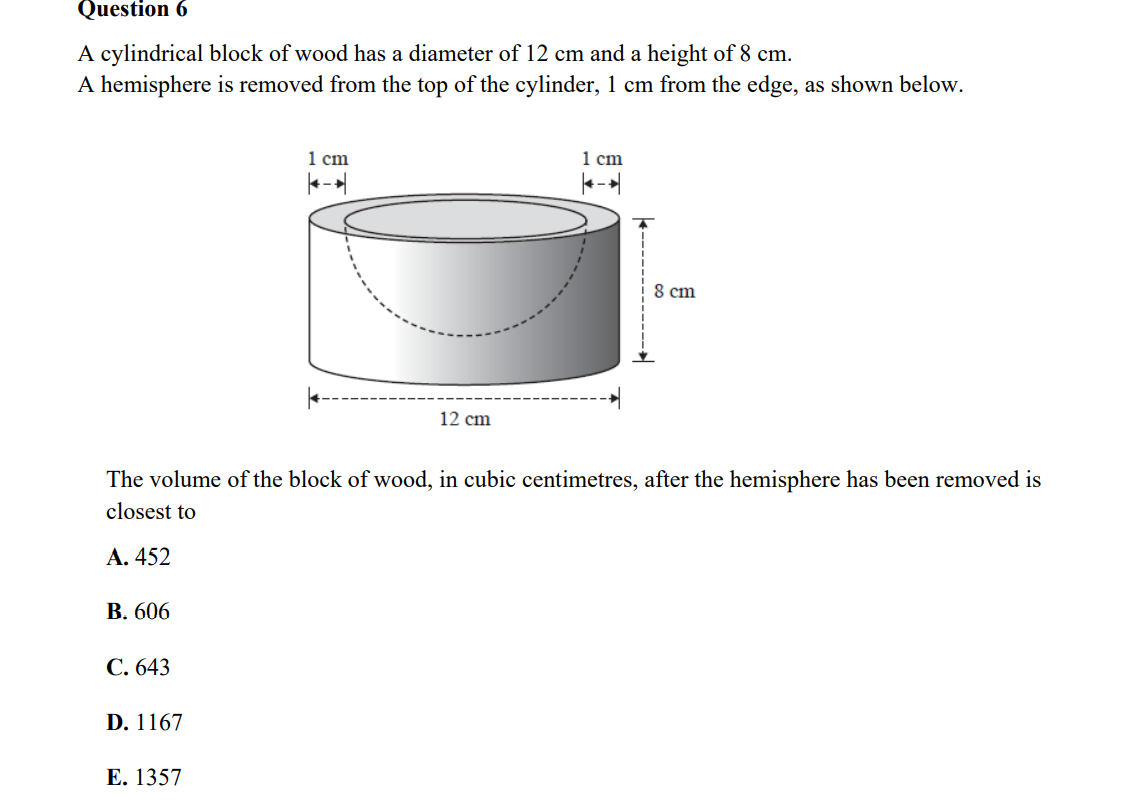
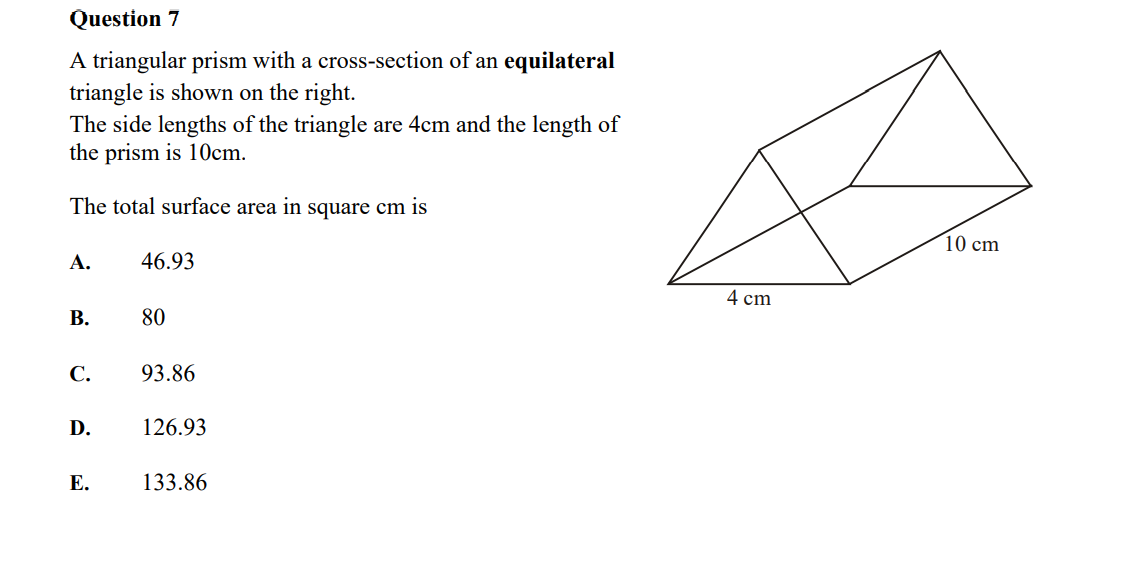
Question: SEND: Work for Submission for Week 2 Show the essential working in the spaces provided for ALL questions. A search and rescue helicopter shines a


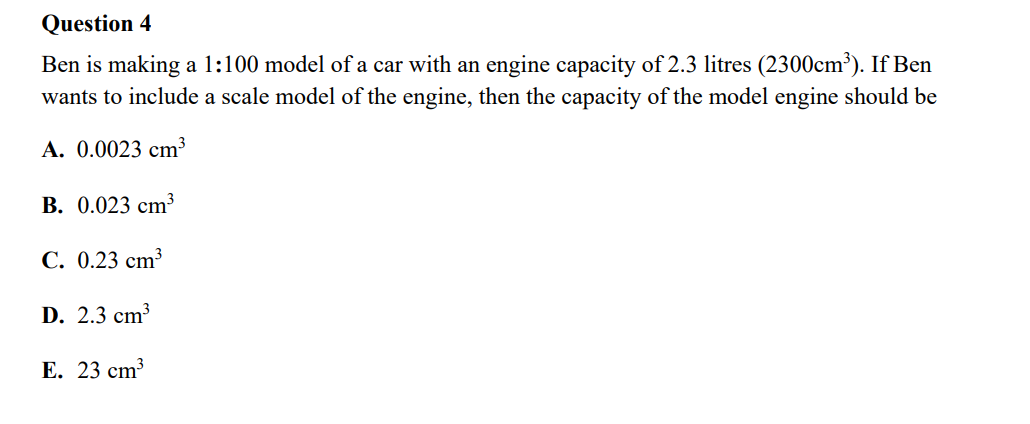




Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


