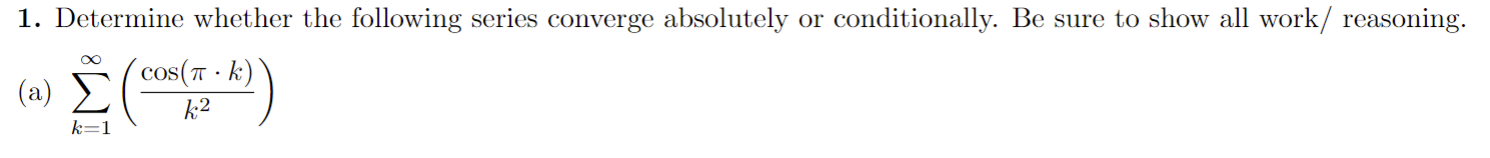
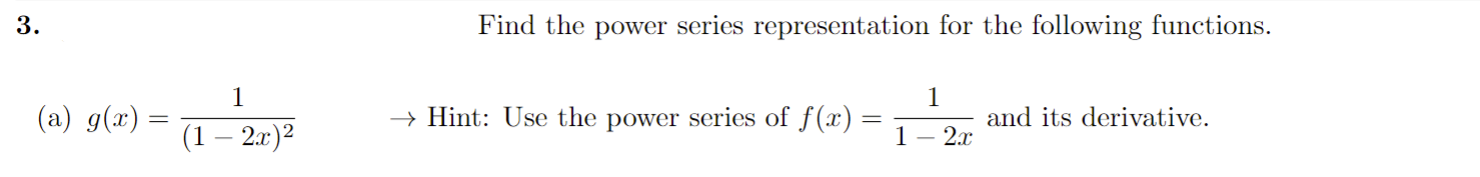
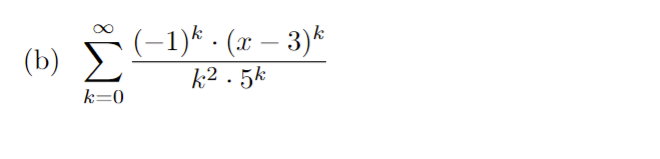
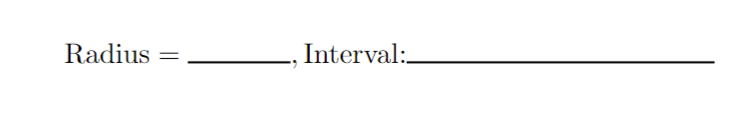
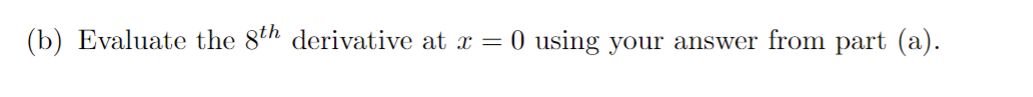
series convergence

note: please try to answer hand-written and in good handwriting.

1.

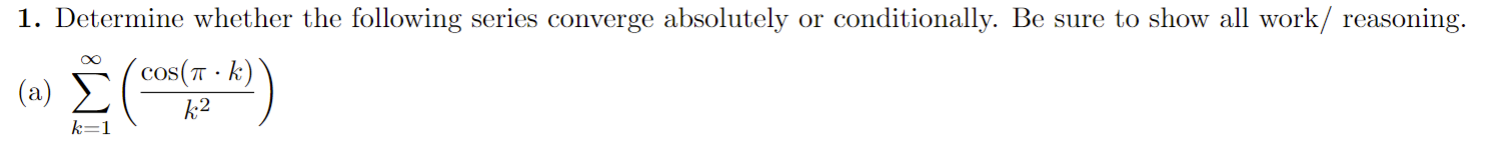
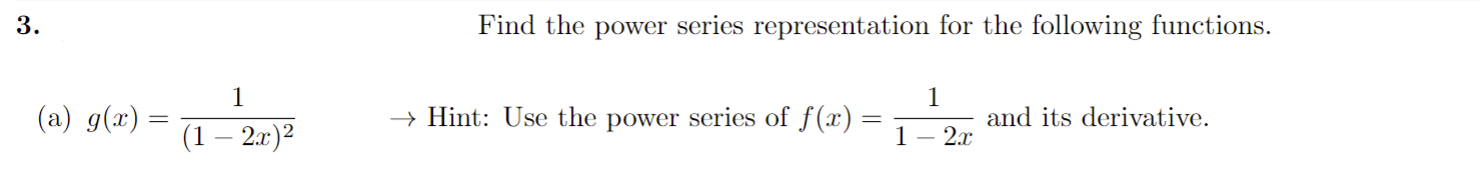
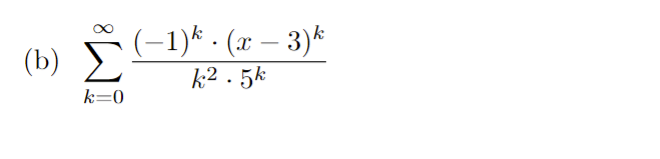
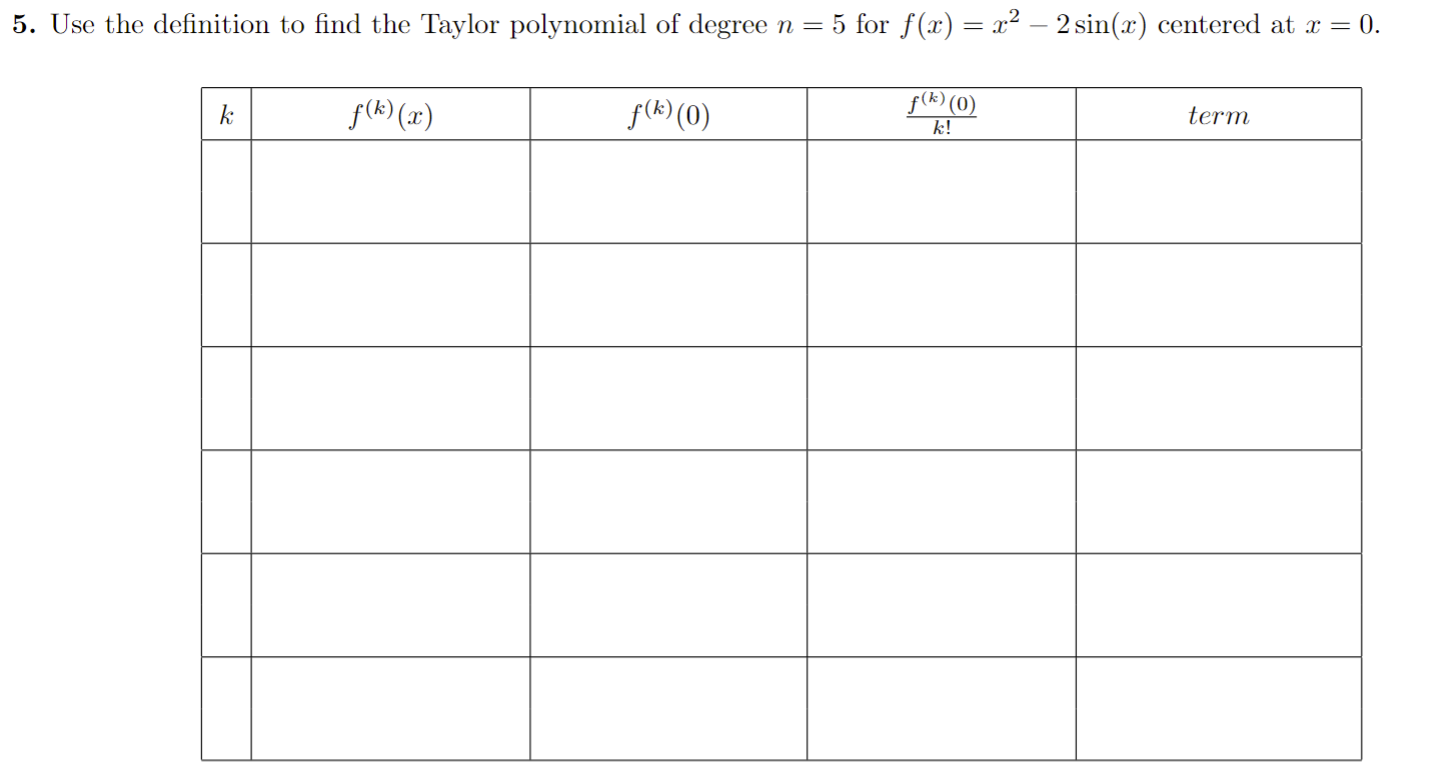
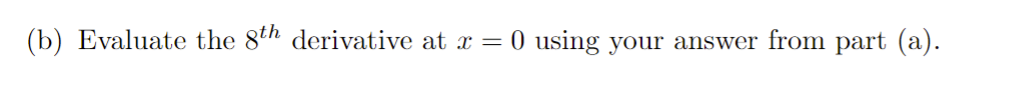
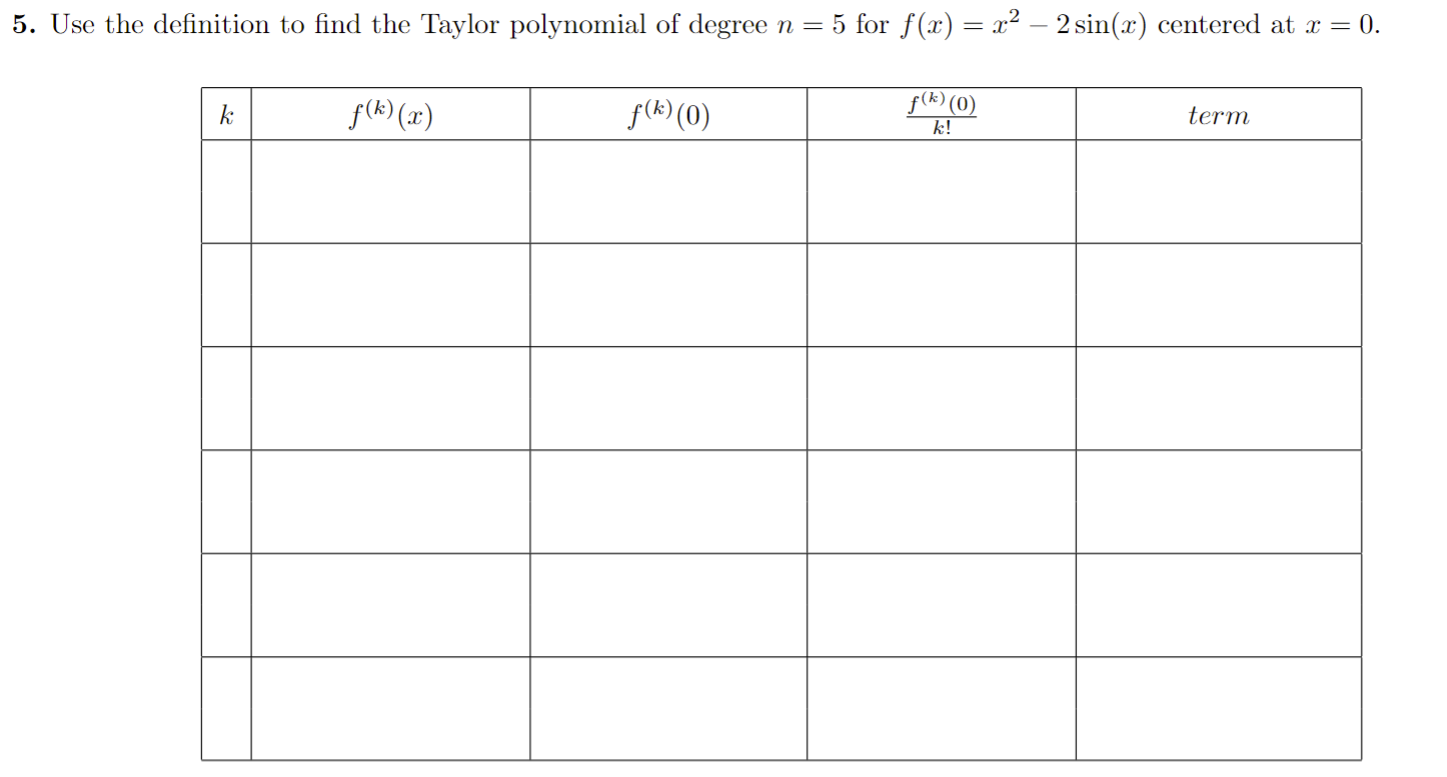
1. Determine whether the following series converge absolutely or conditionally. Be sure to show all work / reasoning. (a) E COS( TT . K) K2 k=1(b) (-1 ) k In (k) k=2y" 1 2. Recall the geometric power series 1 - x for x Hint: Use the power series of f (x) = = 1 - 2x and its derivative.(b) h(x) = In(1 + x2) -> Hint: Use the power series of f (x) = 1 + 22 and its integral.4.Find the radius and interval of convergence for the following series: OO yel (a) 3k . 13 k=0Radius = Interval:(b) E (-1)k . (x - 3)k 12 . 5k k=0Radius = Interval:5. Use the definition to find the Taylor polynomial of degree n = 5 for f(x) = x2 - 2 sin(x) centered at x = 0. term k f ( k ) ( 2 ) f ( k:) (0 ) f ( k) (0) k!6. Derivatives of higher order can be very time consuming - especially for functions like f(x) = x3 . e-. Evaluating such derivatives become very manageable/time efficient problems by using the Taylor polynomials/series. (a) Write the 10th degree Taylor polynomial for f(x) = x5 . e-2: centered at x = 0.(b) Evaluate the 8th derivative at x = 0 using your answer from part (a).Here are some important power series that we have seen and derived. The first three series are derived by using the structure of geometric series, and the last three are derived by using Taylor polynomial definition. These series representations, especially the last three ones, are a powerful tool to write power series for a lot of different functions. (1) 00 1 - x =1tata ta'+ . ..txt ...= n=0 (2) In(1 + x) = x OO + 3 4 + .. + (-1)n+127 n +... = 7 1x|