Question: Set 17 Problem 3 to mirror M Glass container Source M2 One of the beams of an interferometer passes through a small glass cell containing

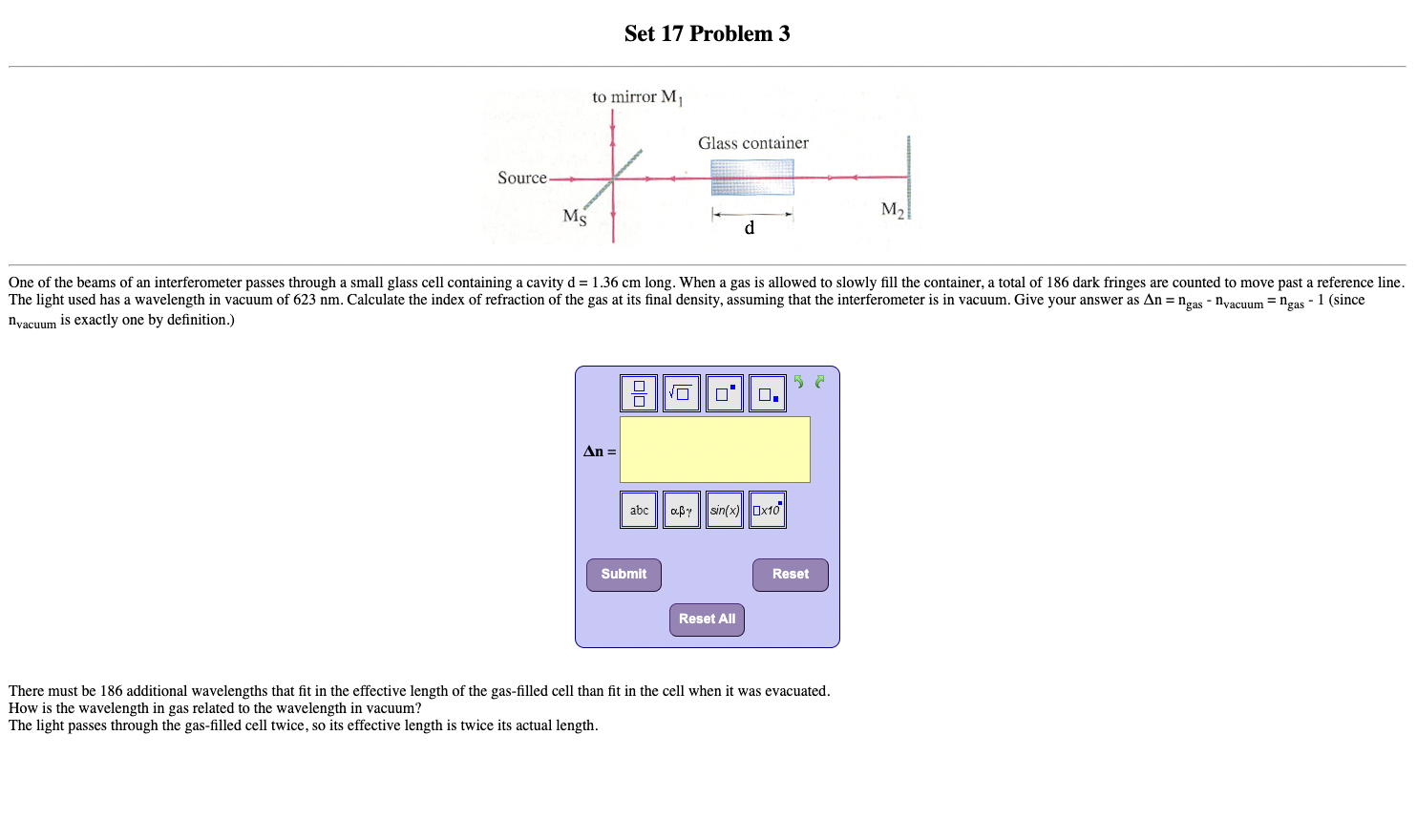
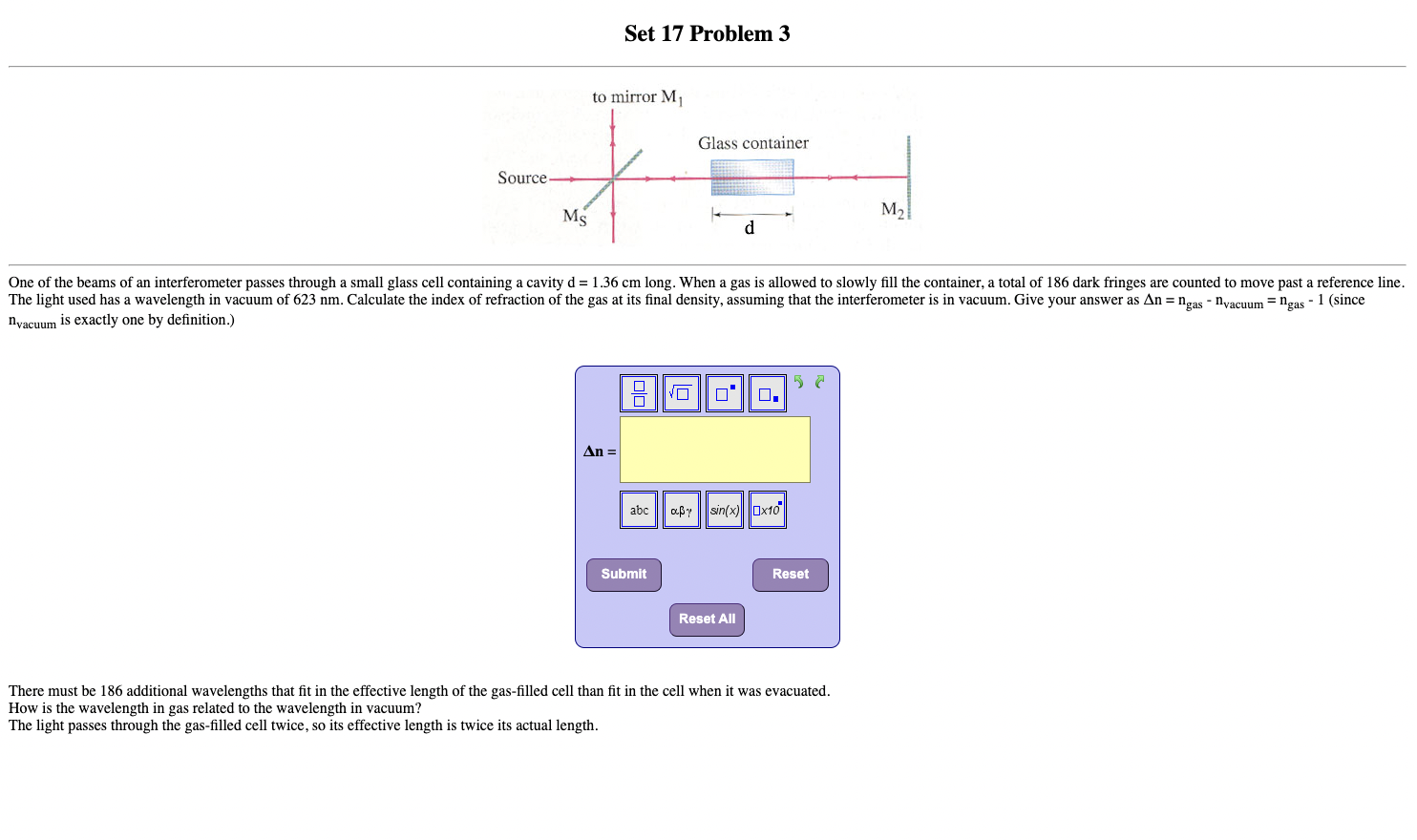
Set 17 Problem 3 to mirror M Glass container Source M2 One of the beams of an interferometer passes through a small glass cell containing a cavity d = 1.36 cm long. When a gas is allowed to slowly fill the container, a total of 186 dark fringes are counted to move past a reference line. The light used has a wavelength in vacuum of 623 nm. Calculate the index of refraction of the gas at its final density, assuming that the interferometer is in vacuum. Give your answer as An = gas - vacuum = gas - 1 (since "vacuum is exactly one by definition.) JC An = abc sin(x Ox10 Submit Reset Reset All There must be 186 additional wavelengths that fit in the effective length of the gas-filled cell than fit in the cell when it was evacuated. How is the wavelength in gas related to the wavelength in vacuum? The light passes through the gas-filled cell twice, so its effective length is twice its actual length

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Physics Questions!

You receive an anonymous tip that your controller is embezzling assets from your company. You begin your investigation by interviewing several employees in the accounting department, who report no...

Set 17 Problem 3 to mirror M1 Glass container Source- Ms M2 d One of the beams of an interferometer passes through a small glass cell containing a cavity d = 1.36 cm long. When a gas is allowed to...

13.8 DIVISION OF AMPLITUDE. MICHELSON+ INTERFEROMETER Interference apparatus may be conveniently divided into two main classes, those based on division of wave front and those based on division of...

One of the beams of an interferometer (Fig. 24-59) passes through a small glass container containing a cavity 1.30cm deep. When a gas is allowed to slowly fill the container, a total of 236 dark...

One of the beams of an interferometer (Fig. 24-61) passes through a small evacuated glass container 1.155 cm deep. When a gas is allowed to slowly fill the container, a total of 158 dark fringes are...

Fraction of hosts infected Case Study 2 Hosts, Parasites, and Time-Travel 0.8 0.6 0.4 0.2 0 Past Contemporary Future Time Figure \u00031 Horizontal axis is the time from which the parasite was taken,...

Select an organisation with which you are familiar and write a report on how you would transform a clearly defined segment of the organisation into a sustainable business segment. Do not select an...

Coding Language c++ Huffman Encoding Using the Huffman encoding algorithm as explained in class, encode and decode the Speech.txt file using frequency tree and priority queue. Implement Huffman style...

can you please help put this in google slide with image and pleas leve the link so i can have access to the google slide pls Step 1: Let's focus on the question "How does a dentist's lamp work?" and...

Supply Chain Management Introduction Outline What is supply chain management? Significance of supply chain management. Push vs. Pull processes utdallas.edu/~metin 1 A Generic Supply Chain Sources:...

Solutions from Montgomery, D. C. (2012) Design and Analysis of Experiments, Wiley, NY Chapter 6 k The 2 Factorial Design Solutions 6.1. An engineer is interested in the effects of cutting speed (A),...

Think about how you would answer the following question. Next Wednesdays meeting has been moved forward two days. What day is the meeting now that it has been rescheduled? This question is ambiguous,...

When auditors use The Risk-Based Audit Approach, there are four-step to approach control evaluation. They are as follows : 1) Determine the threats facing the accounting information systems (AIS). 2)...

2. Which of the following statements can be used to code a loop whose instructions you want processed 10 times? a. Do...Loop b. For...Next c. either a or b

A particle with mass m moves in a potential U(x) = A |x|, where A is a positive constant. In a simplified picture, quarks have a potential energy of interaction of approximately this form, where x...

(a) Show by direct substitution in the Schrodinger equation for the one-dimensional harmonic oscillator that the wave function 1 (x) = A1xe a2x2/2, where a2 = mw/h, is a solution with energy...

A ¾ -in-thick steel bar, to be used as a beam, is welded to a vertical support by two fillet welds as illustrated. (a) Find the safe bending force F if the permissible shear stress in the...

A bar of steel has the minimum properties Se = 276 MPa, Sy = 413 MPa, and Sut = 551 MPa. The bar is subjected to a steady torsional stress of 103 MPa and an alternating bending stress of 172 MPa....

Suppose that the time to failure T of a certain hinge is an exponential random variable with probability density f (t) = ? c ?? t , t > 0. From prior experience we are led to believe that. 0 is a...

Write a paragraph discussing what your favorite number is and why it is your favorite number. (Your paragraph should be properly formatted and have at least five sentences.)

The status rule: We tend to have more confidence in information presented by someone who has a relatively high status and rank in society than by someone who hasnt.

The spatial rule: The closer spatial proximity we have to an event, the more importance we will attach to it.

The visual rule: If we observe an event with our own eyes, we will attach more weight to it than if someone else had described it to us.