Setup

Consider the following model setup somewhat analogous to Shleifer and Vishny (1997).

There are three periods, labeled 1, 2 and 3, and there is only one asset, a stock available in one unit net supply. There are two types of participants: noise traders and arbitrageurs. At time 3 all participants realize the fundamental value of the asset and the asset is liquidated at a price P₃ = v. Since the price is equal to v at t = 3 for sure, there is no long run fundamental risk in this stock. The value v can be either v^H or v^L and becomes known to arbitrageurs at time 2; whereas both possibilities are considered equally likely at time 1. Noise traders, however, misestimate the expected value at time t of the asset by some sentiment shock S_t , i.e., 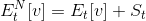_. Our convention is that positive S_t denotes optimism and negative S_t pessimism. Hence aggregate noise trader demand is given by:

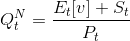
Arbitrageurs are risk-neutral and fully rational and take positions against the mispricing generated by the noise traders. Arbitrageurs have cumulative resources under management F_t , meaning the maximum position size they may take (long or short) can have value up to F_t .

Question

Suppose that S_t = S > 0 in both periods 1 and 2. Also take F₂ as given and suppose F₂ is never large enough for arbitrageurs to be able to bring prices to fundamental value. Assume that arbitrageurs invest all of F₂ in the stock. Write down an expression for the demand 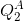of arbitrageurs at t=2. Then use this expression along with the equation for 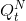above to solve for the price at t=2, P₂(v), as a function of v (= v^H or v^L ) and in terms of the parameters S and F₂. (Hint: Calculate aggregate demand. We know aggregate supply. What is the market clearing equilibrium price?)

EN [] = E?[0] + St EN [] = E?[0] + St