Show completely your steps for the solution and make it clearly readable.

Q1: Use the Bellman-Ford (Distance Vector) algorithms to find the set of shortest paths from all nodes to the destination at node 6

Q2:Use the Dijkstra (Link State) algorithm to find the set of shortest paths from node 1 to all other nodes, and give the resulting routing diagrams as seen from node 1.

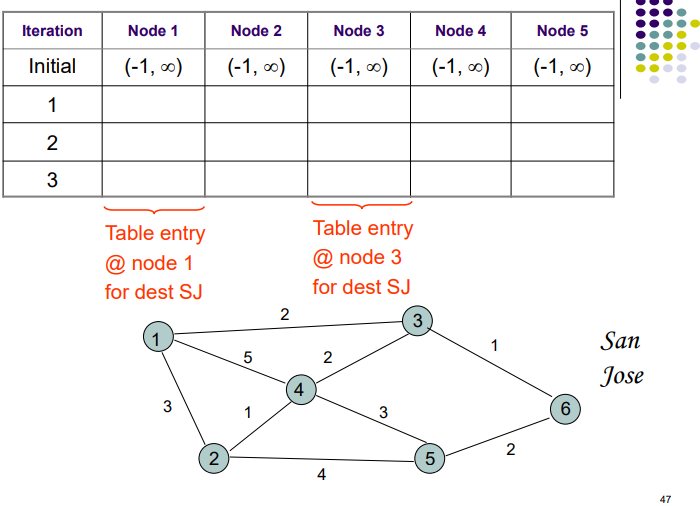
\begin{tabular}{|c|c|c|c|c|c|} \hline Iteration & Node 1 & Node 2 & Node 3 & Node 4 & Node 5 \\ \hline Initial & (1,) & (1,) & (1,) & (1,) & (1,) \\ \hline 1 & & & & & \\ \hline 2 & & & & & \\ \hline 3 & & & & & \\ \hline \end{tabular} Table entry Table entry @ node 1 @ node 3 for dest SJ for dest SJ San Jose 47