Show that a probability space contains at most countably many atoms. The definition of an atom is given below.

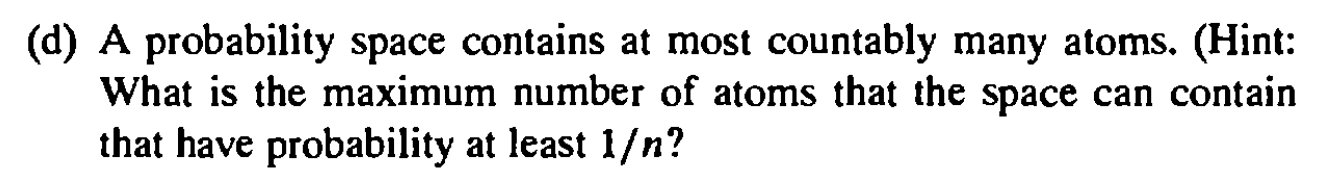
An atom in a probability space ($2, B, P) is defined as (the equivalence class of) a set A E B such that P(A) > 0, and if B C A and B E B, then P(B) = 0, or P(A \\ B) = 0. Furthermore the probability space is called non-atomic if there are no atoms; that is, A e B and P(A) > 0 imply that there exists a B E B such that B C A and 0