Show that a set

A

is totally bounded in the space

\\\\omega

if and only if there exists a sequence\

(C_(n))_(n)=1^(\\\\infty )

of positive numbers such that

|x_(n)|

for all

x=(x_(n))_(n)=1^(\\\\infty )inA

.

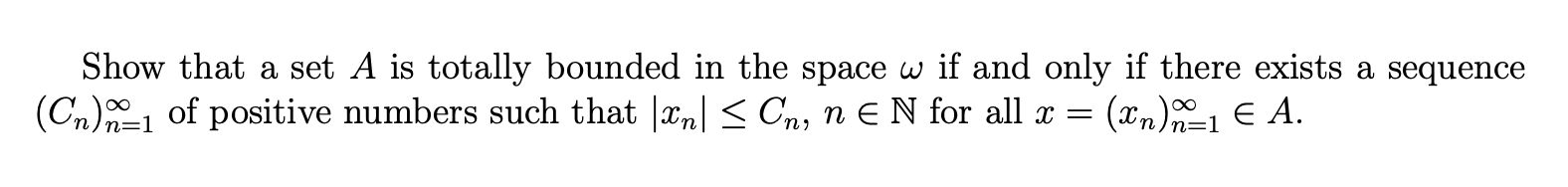
Show that a set A is totally bounded in the space if and only if there exists a sequence (Cn)n=1 of positive numbers such that xnCn,nN for all x=(xn)n=1A