Question: Show that any computable function (specified by its number with respect to a fixed Godel universal function), one can effectively find infinitely many natural numbers
Show that any computable function 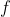 (specified by its number with respect to a fixed Godel universal function), one can effectively find infinitely many natural numbers each of which is either a fixed point of
(specified by its number with respect to a fixed Godel universal function), one can effectively find infinitely many natural numbers each of which is either a fixed point of 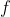 or a point at which
or a point at which 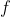 is undefined. (Hint: for an arbitrary computable function there exists a unary total computable function
is undefined. (Hint: for an arbitrary computable function there exists a unary total computable function 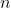 with the property: for each p either the function
with the property: for each p either the function 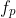 is undefined at the point
is undefined at the point 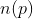 or
or 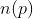 is a fixed point of the function
is a fixed point of the function 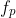 )
)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


