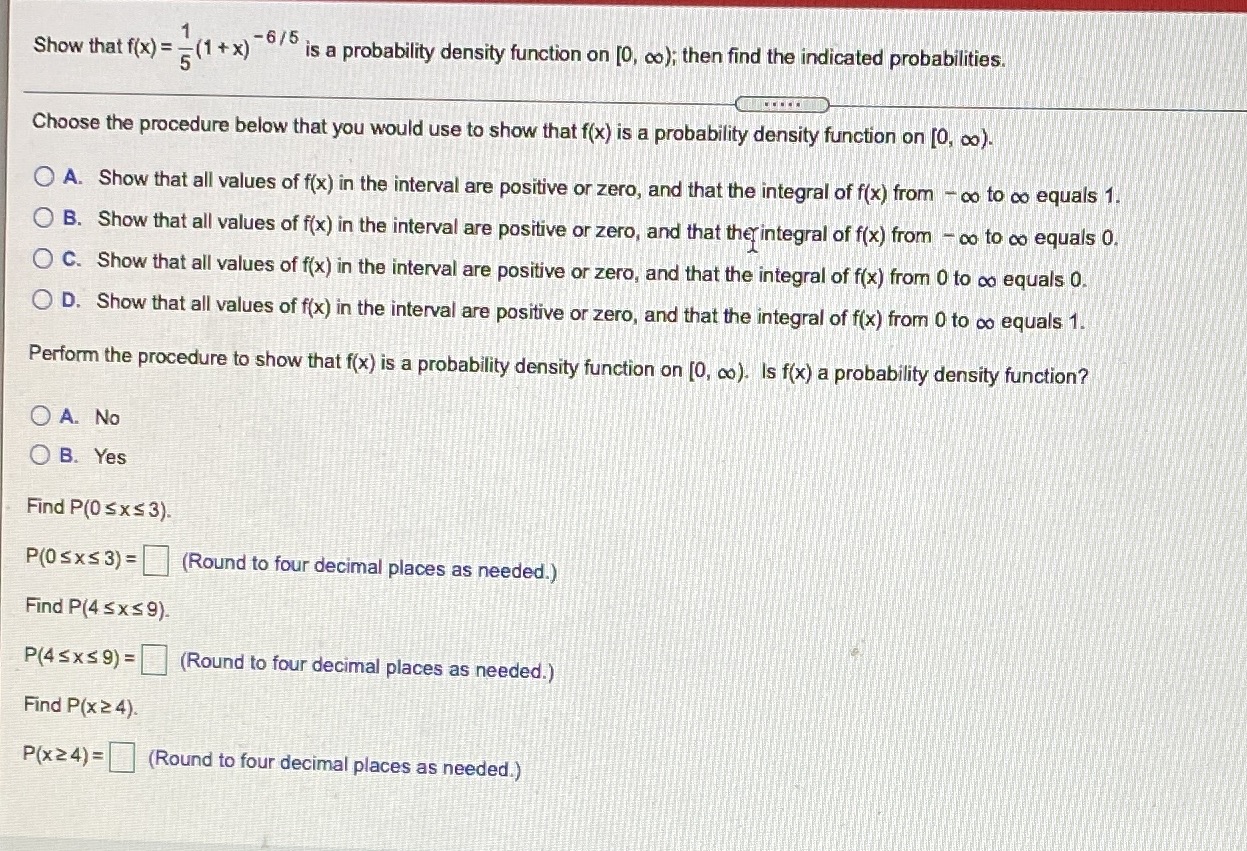
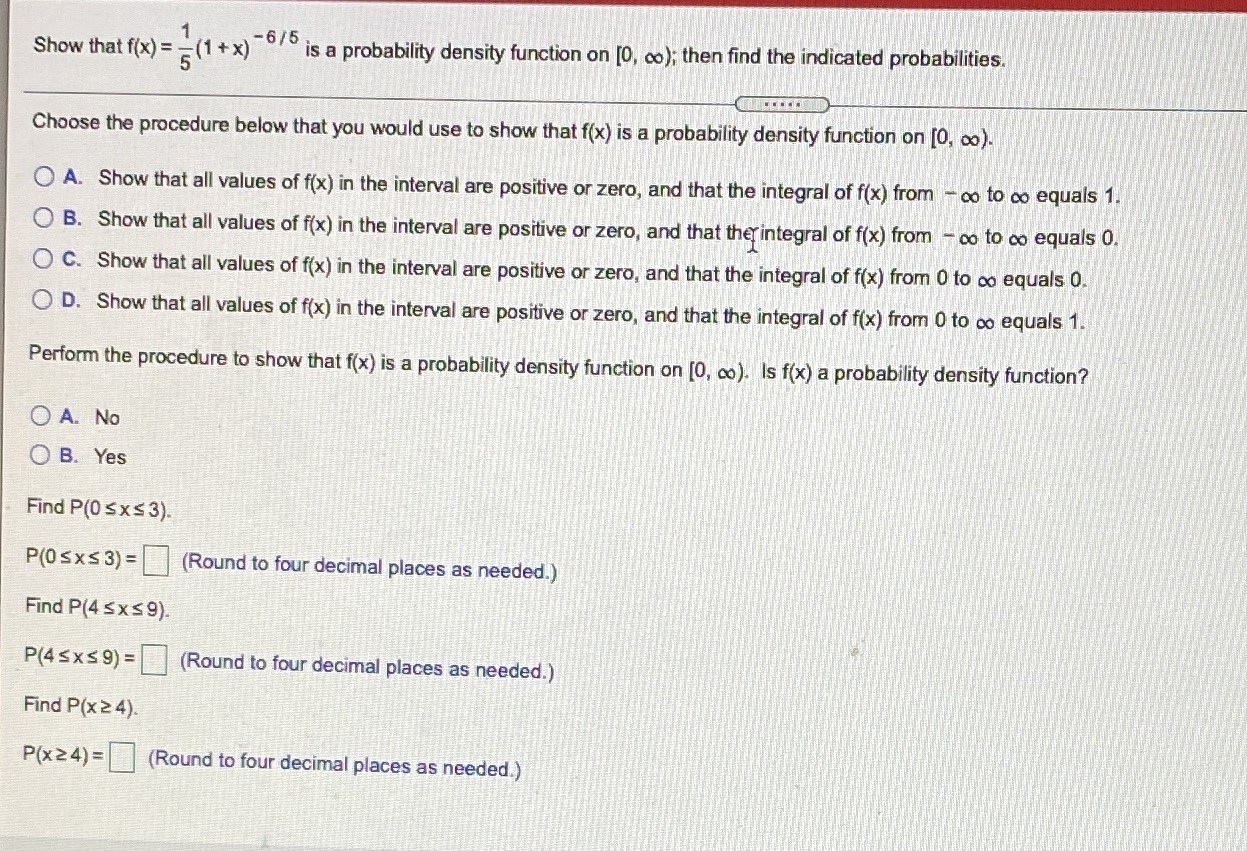
Show that f(x) = = (1 + x) " is a probability density function on [0, co); then find the indicated probabilities. Choose the procedure below that you would use to show that f(x) is a probability density function on [0, co). O A. Show that all values of f(x) in the interval are positive or zero, and that the integral of f(x) from - co to co equals 1. O B. Show that all values of f(x) in the interval are positive or zero, and that ther integral of f(x) from - co to co equals 0. C. Show that all values of f(x) in the interval are positive or zero, and that the integral of f(x) from 0 to co equals 0. O D. Show that all values of f(x) in the interval are positive or zero, and that the integral of f(x) from 0 to co equals 1. Perform the procedure to show that f(x) is a probability density function on [0, co). Is f(x) a probability density function? O A. No O B. Yes Find P(0 S x$ 3). P(0 Sx$ 3) = (Round to four decimal places as needed.) Find P(4 5x$9). P(4 Sx59) = (Round to four decimal places as needed.) Find P(x 2 4). P(x24) = (Round to four decimal places as needed.)