Question: Show that lim _ ( x - > infty ) ( x ^ ( n ) ) / ( e ^ ( x
Show that limxinfty xnex for any positive integer n
Find the values of of the constant k which make fxsinxxpi if xpi k if xpi :
continuous at xpi
Find all values of k and m such that limxkmlnxx
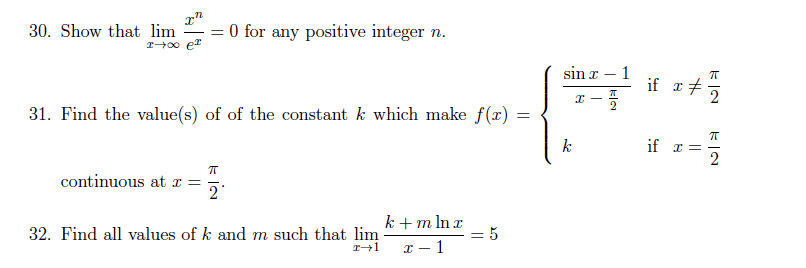
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


