Question: Show that the equation 3x + 2 cos x + 5 = 0 has exactly one real root. Find the smallest possible area of an

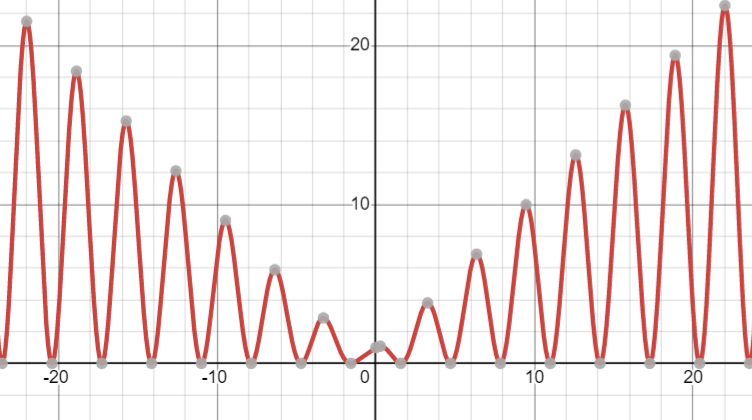
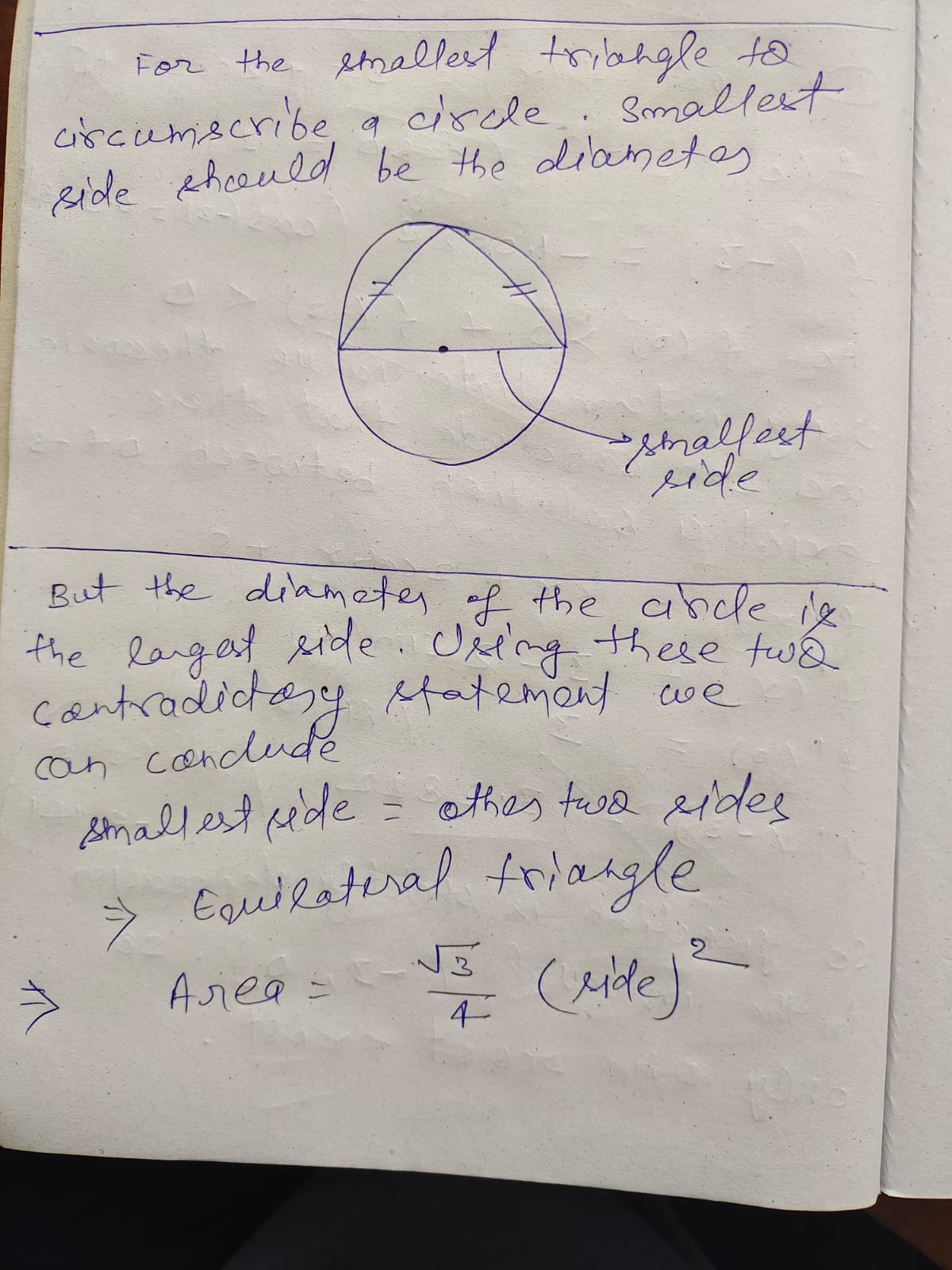
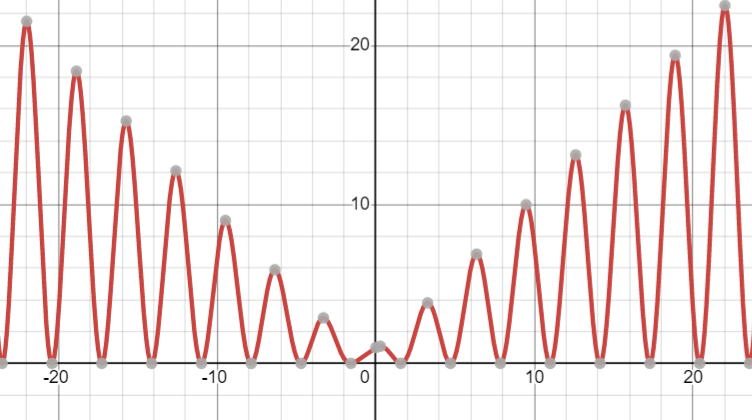
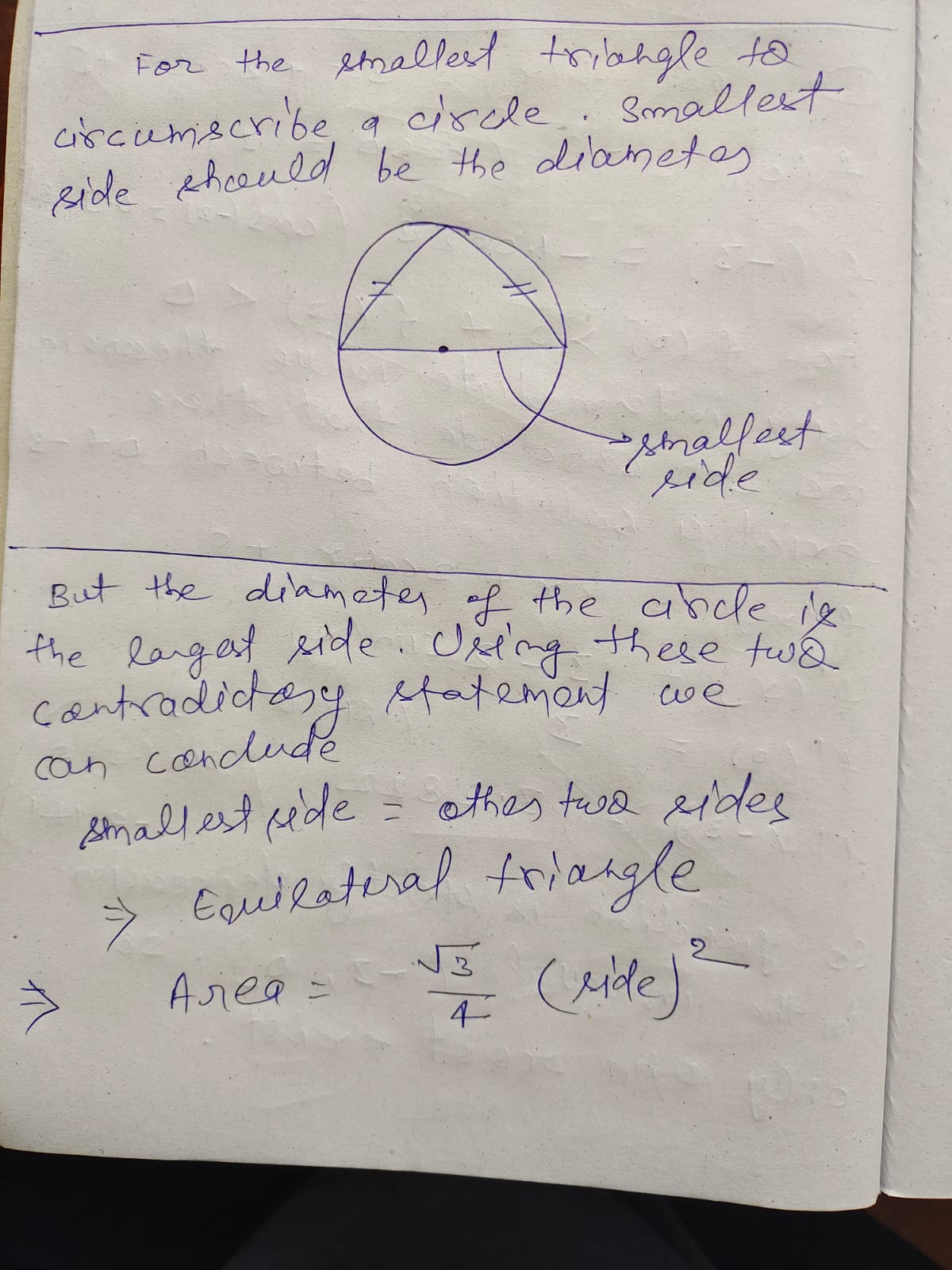
Show that the equation 3x + 2 cos x + 5 = 0 has exactly one real root. Find the smallest possible area of an isosceles triangle that is circumscribed about a circle of radius r. Use the graphs of f, f', and f" to estimate the x-coordinates of the maximum and minimum points and inflection points of f. COS X 41. f(X) = -TEXST VX? + X + 1 42. f (X) = ex In(x? - 1)20 10 -20 -10 0 10 20\ff ( - 1 ) = 3 ( - 1 ) 1. let floc ) = 3se + 2cosxx +s f ( 0 ) = 7 ( caso = 4 ) * ( - 3 ) = - 10028 / Gas ( - 3 ) = 0.9986 As f ( 0 ) > 0 + $ ( - 3 )

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Show that the equation 3x + 2 cos x + 5 = 0 has exactly one real root.

35-38 Produce graphs of f that reveal all the important aspects of the curve. Use graphs of f' and f" to estimate the intervals of increase and decrease, extreme values, intervals of concavity, and...

45. Show that the equation 3x + 2 cos x + 5 = 0 has exactly one real solution

Question 53, 59, 61,65,69,71 Chapter applications of differentiation d 43. Investigate the family of functions f (x) In(sin x + C). What features do the members of this family have in common? How do...

please answer as accurately as possible and show all work according to textbook . Thanks. 4. Let f(x) =3x3 + x 2. a. Find an interval where the function f has one root. b. Use Rolle's theorem to show...

3.) Show that the equation 3x + 2 cosx -|- 5 = 0 has exactly one real root. (x)= 3x+ 2405x+5 is continuous on (-20,20) and f /0) = 0+ 2+5 =7 70 .: By the int. Value theorem, $/-1)= -317 -2+5 : - 311...

Written Assignment 1. An airplane is flying towards a radar station at a constant height of 6 km above the ground. If the distance s between the airplane and the radar station is decreasing at a rate...

SECTION 4.2 THE MEAN VALUE THEOREM - I 4.2 THE MEAN VALUE THEOREM A Click here for answers. S Click here for solutions. 1-4 - Verify that the function satisfies the three hypotheses of 9. f(x) = 1/x;...

(Will not be accepted without staple) [First Name] [Last Name] Math-2417, thq 05, 17-09-16, 14:59 [Net ID] [Problem Section] Instructions: 1. Fill in the requested information on the line above. 2....

Name two ways to identify the tasks that need to be accomplished over the course of a project.

B (12 Total). Marshall Junior was born on August 1 of this year. Current college costs are about $20,000 per year and rising at about 5% annually. 1. How much will college cost Marshall Jr's Freshman...

Compute the integral: 0 5 6 x + 1 5 x 2 + 5 x + 1 2 d x

Norris Corporation issued $2,000,000 in 10.5 percent, 10-year bonds on February 1, 2014, at 104. Semiannual interest payment dates are January 31 and July 31. Use the straight-line method and ignore...

Kestral Manufacturing identified the following overhead costs and cost drivers for the current period. Kestral produces customized products that move through several different processes. Materials...

Palmer Company uses an activity-based costing system. It has the following manufacturing activity areas; related drivers used as allocation bases, and cost allocation rates: During the month, 100...

Applewood Electronics manufactures two large-screen television models, the Monarch, which has been produced for five years and sells for $900, and the Regal, a new model that sells for $1,140....

On January 2, 2013, Sanborn Tobacco Inc. bought 5% of Jackson Industry's capital stock for $90 million as a temporary investment. Sanborn classified the securities acquired as available-for-sale....

Create a 200 word summary on the Juvenile Justice System than and today. Describe The Juvenile system and provide a generalizable definition. Highlight the issues in the Juvenile system and why this...

Plant and equipment was purchased on 1 January 2012 for $ 30,000$, when the relevant specific price index was 90 . What is the current cost value of the asset at 31 December 2013 if the index at that...

A The plant and equipment, details of which are given in Question 30.4, is depreciated on a straight line basis at $10 \%$ per annum. The depreciation charge is based on year-end values. What is the...

Assess how the eight principles of the UK Data Protection Act (www.gov.uk/data-protection) relate to actions that ecommerce managers need to take to ensure legal compliance of their site.