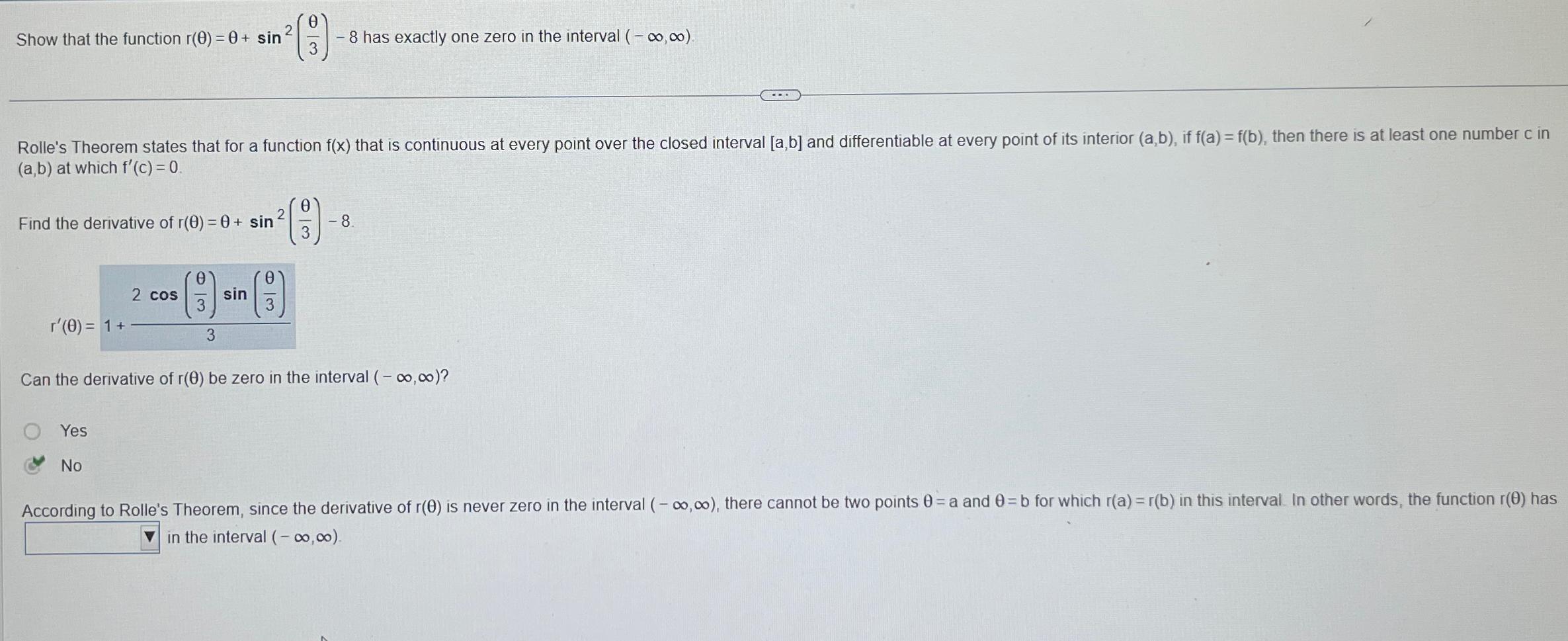
Show that the function r(0) = 0 + sin (9) - 8 has exactly one zero in the interval ( - , 0) Rolle's Theorem states that for a function f(x) that is continuous at every point over the closed interval [a,b] and differentiable at every point of its interior (a,b), if f(a) = f(b), then there is at least one number c in (a,b) at which f'(c) = 0. Find the derivative of r(0)=0+ sin 2 -8 3 2 cos sin 3 r'(0) = 1+ 3 Can the derivative of r(0) be zero in the interval (-00,00)? Yes No According to Rolle's Theorem, since the derivative of r(e) is never zero in the interval (-00,00), there cannot be two points 0 = a and 0=b for which r(a) = r(b) in this interval. In other words, the function r(0) has in the interval (-00,00).