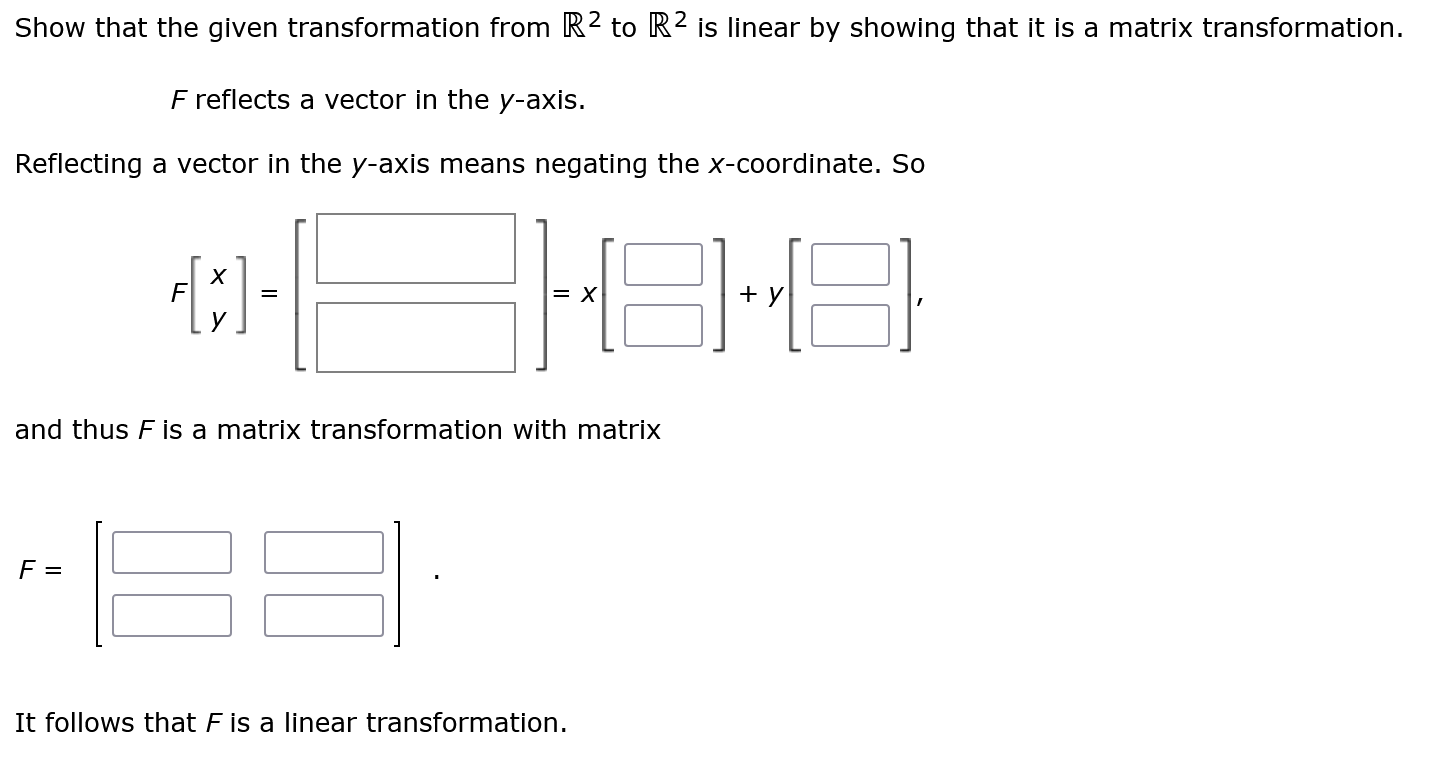
Question: Show that the given transformation from R^(2) to R^(2) is linear by showing that it is a matrix transformation. F reflects a vector in the
Show that the given transformation from
R^(2)to
R^(2)is linear by showing that it is a matrix transformation.\
Freflects a vector in the
y-axis.\ Reflecting a vector in the
y-axis means negating the
x-coordinate. So\
F[[x],[y]]=[]=x[]+y[1]\ and thus
Fis a matrix transformation with matrix\
F=[[|,|]]. \ It follows that
Fis a linear transformation.
Show that the given transformation from R2 to R2 is linear by showing that it is a matrix transformation. F reflects a vector in the y-axis. Reflecting a vector in the y-axis means negating the x-coordinate. So F[xy]=[]=x[]+y[], and thus F is a matrix transformation with matrix F=[]. It follows that F is a linear transformation
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


