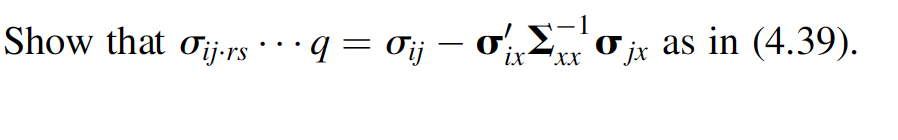
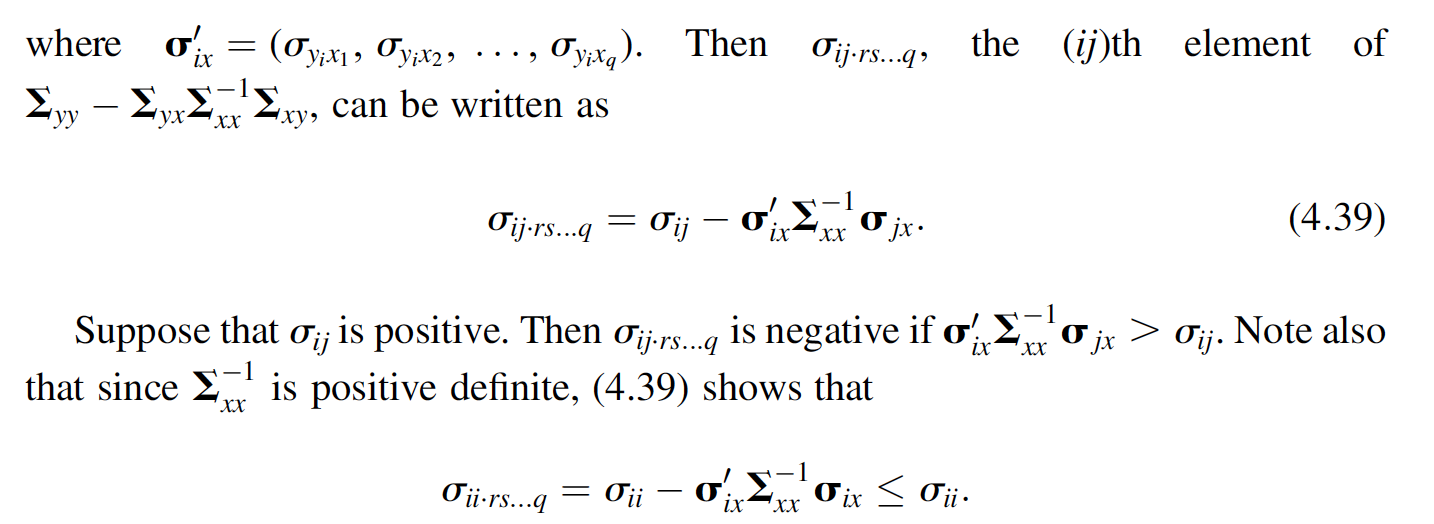
Show that Tijers --- 9 = 0; - 'Cjx as in (4.39). We now define the partial correlation of y; and y; adjusted for a subset of other y vari- ables. For convenience, we use the notation of Theorems 4.4c and 4.4d. The subset of y's containing y; and y; is denoted by y, and the other subset of y's is denoted by x. Let v be Np+q(m, 2) and let v, j, and be partitioned as in Theorem 4.4c and 4.4d: V = (3) u= My Mix xy , Yq are all the Exy. For The covariance of and y; in the conditional distribution of y given x will be denoted by Oij.rs...q> where y; and y; are two of the variables in y and yr, Ys, ..., variables in x. Thus Oij.rs.... is the (ij)th element of cov(y|x) = Eyy Ex'Exy. example, 013.567 represents the covariance between y and yz in the conditional dis- tribution of y, Y2, Y3, y4 given y5, Yo, and yz [in this case x = (75, 76, yn)']. Similarly, 022.567 represents the variance of y2 in the conditional distribution of y1, y2, 73, 74 given y5, 96, Y7. We now define the partial correlation coefficient Pij.rs..., to be the correlation between yi and Y; in the conditional distribution of y given X, where x = (yr, Ys, yg)'. From the usual definition of a correlation (see (3.19)], we can obtain Pij.rs...q from Oij.rs...q: Pij.rs...q Oij.rs...q Oiirs... qjj.rs... (4.36) ...q is = This is the population partial correlation. The sample partial correlation rij.rs discussed in Section 10.7, including a formulation that does not require normality. The matrix of partial correlations, P, (Pij-rs...) can be found by (3.30) and (4.27) as D2y.D., (4.37) yor yox yor yor? - where Eyx = cov(y|x) = {wy Ex'Exy and Dyx [diag({y.x)]"/2. Unless y and x are independent (Eyx O), the partial correlation Pij.rs.... is differ- ent from the usual correlation Pij = 0;;/ VojOjj. In fact, S...q and Pij can be of oppo- site signs (for an illustration, see Problem 4.16 g, h). To show this, we express Oij.rs...q in terms of oij. We first write Eyx in terms of its rows 1x Oyx1 Ty2x1 Oyx2 Oy2x2 Oyxq y2Xq 2x Fyx = cov(y, x) = (4.38) : OypX1 Oypx2 px the (ij)th element of ...) Oij.rs...q; where o'r = (oy Tyixi, 1, Oy;x22 Oyixq). Then . can be written as yy yx XX -Xy, Tij.rs... = Cij o, Sa'dit (4.39) Suppose that 0;; is positive. Then Oijir... is negative if o d'O jx > Oij. Note also that since - is positive definite, (4.39) shows that -1 Oii.rs...q = Oji ix where y; and y; are two of the variables in y and yr, Ys, ..., variables in x. Thus Oij.rs.... is the (ij)th element of cov(y|x) = Eyy Ex'Exy. example, 013.567 represents the covariance between y and yz in the conditional dis- tribution of y, Y2, Y3, y4 given y5, Yo, and yz [in this case x = (75, 76, yn)']. Similarly, 022.567 represents the variance of y2 in the conditional distribution of y1, y2, 73, 74 given y5, 96, Y7. We now define the partial correlation coefficient Pij.rs..., to be the correlation between yi and Y; in the conditional distribution of y given X, where x = (yr, Ys, yg)'. From the usual definition of a correlation (see (3.19)], we can obtain Pij.rs...q from Oij.rs...q: Pij.rs...q Oij.rs...q Oiirs... qjj.rs... (4.36) ...q is = This is the population partial correlation. The sample partial correlation rij.rs discussed in Section 10.7, including a formulation that does not require normality. The matrix of partial correlations, P, (Pij-rs...) can be found by (3.30) and (4.27) as D2y.D., (4.37) yor yox yor yor? - where Eyx = cov(y|x) = {wy Ex'Exy and Dyx [diag({y.x)]"/2. Unless y and x are independent (Eyx O), the partial correlation Pij.rs.... is differ- ent from the usual correlation Pij = 0;;/ VojOjj. In fact, S...q and Pij can be of oppo- site signs (for an illustration, see Problem 4.16 g, h). To show this, we express Oij.rs...q in terms of oij. We first write Eyx in terms of its rows 1x Oyx1 Ty2x1 Oyx2 Oy2x2 Oyxq y2Xq 2x Fyx = cov(y, x) = (4.38) : OypX1 Oypx2 px the (ij)th element of ...) Oij.rs...q; where o'r = (oy Tyixi, 1, Oy;x22 Oyixq). Then . can be written as yy yx XX -Xy, Tij.rs... = Cij o, Sa'dit (4.39) Suppose that 0;; is positive. Then Oijir... is negative if o d'O jx > Oij. Note also that since - is positive definite, (4.39) shows that -1 Oii.rs...q = Oji ix