Question: Show that V = {(a, b) a, b R} with addition defined by (a1, a2)+(b1, b2) = (a1b1, 0) and scalar multiplication is defined as

  1. Show that V = {(a, b) a, b R} with addition defined by (a1, a2)+(b1, b2) = (a1b1, 0)
  2. and scalar multiplication is defined as c(a1, a2) = (ca1, ca2) is not a vector space. In
  3. addition list all of the axioms that fail.

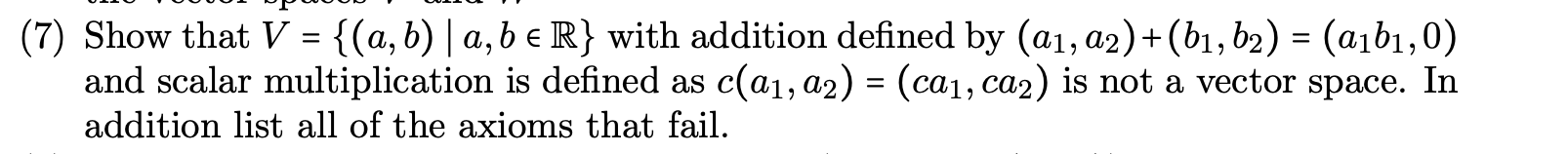
Show that V = {(a, b) a, b R} with addition defined

(7) Show that V = {(a, b) | a, be R } with addition defined by (a1, a2) + (b1, b2) = (a1b1, 0) and scalar multiplication is defined as c(a1, a2) = (cal, ca2) is not a vector space. In addition list all of the axioms that fail

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Q:

Please help me solve these weekly practice questions. Please also provide the work, number and section. The sections are : From Additional Exercises ending Section 6.1:Exercises # 6.1.2 ; 6.1.3 ;...

Q:

In this assignment, you are given the cpp file HW2.cpp, which contains a prototype of the class Mat22. Basically, the class is a structure for 2 by 2 matrices the integers a,b,c, and d represent the...

Q:

Q4 (6 points) F = Q x Q, with addition and multiplication defined as follows: (a1, b1) + (a2, b2) = (a1 + a2, b + b2), (a1,b1) (a2, b2) = (a,a2 bb2, a,b2 + azb). a) Show that F is a field. b) Show...

Q:

4 This assignment, based on the content of Unit 4 of the Study Guide, is worth 3% of your grade. We recommend that you hand it in after you complete Unit 4. You must show all of your work in order to...

Q:

Implement the functions in Exercises.hs. There are 17 of these (labeled like #1), worth 5 points each. The first five concern Functor, and mostly require implementing fmap for types I define. The...

Q:

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

Q:

chapter 5 INTRODUCTION TO MATRIX ALGEBRA GOALS The purpose of this chapter is to introduce you to matrix algebra, which has many applications. You are already familiar with several algebras:...

Q:

chapter 5 INTRODUCTION TO MATRIX ALGEBRA GOALS The purpose of this chapter is to introduce you to matrix algebra, which has many applications. You are already familiar with several algebras:...

Q:

Find N(A) and describe it as all linear combinations of some vectors (you must find these vectors). A = 0 4 Find N( A) and describe it as all linear combinations of some vectors (you must find these...

Q:

BA 1605: Midterm Recap (Due: Feb. 27, 2015) Name _____________________________ 50 Student ID _____________________________ Section 01B 10:00~11:20 am Section 02B 01:00~02:20 pm [Questions 4 ~ 7] The...

Q:

In Fig P6.101 a thick filter is being tested for losses. The flow rate in the pipe is 7 m3/min and the upstream pressure is 120 kPa. The fluid is air at 20°C. Using the water manometer reading,...

Q:

Consider Prob. 3. If the mapping X- X' given by z f is surjective, show that X must be a Hilbert space.

Q:

If an analyst estimates a quality of earnings ratio of 0 . 8 , what does this imply about the company? Group of answer choices The company may be aggressive in its revenue recognition policy The...

Q:

Martin Jackion recelvei an hourly wage rate of S15, with time and a half far all hours worked in excess of 40 hours duripg a weeki. Payron data tor the current weck ace as follons: hourn worked, 45;...