Question: Show using Fourier analysis that the implicit Cranck-Nicholson scheme (k+1) _ uj (k) ( k) Uj_1 - 2u, (k) (k) (k+1) uj + Uit1 (k+1)

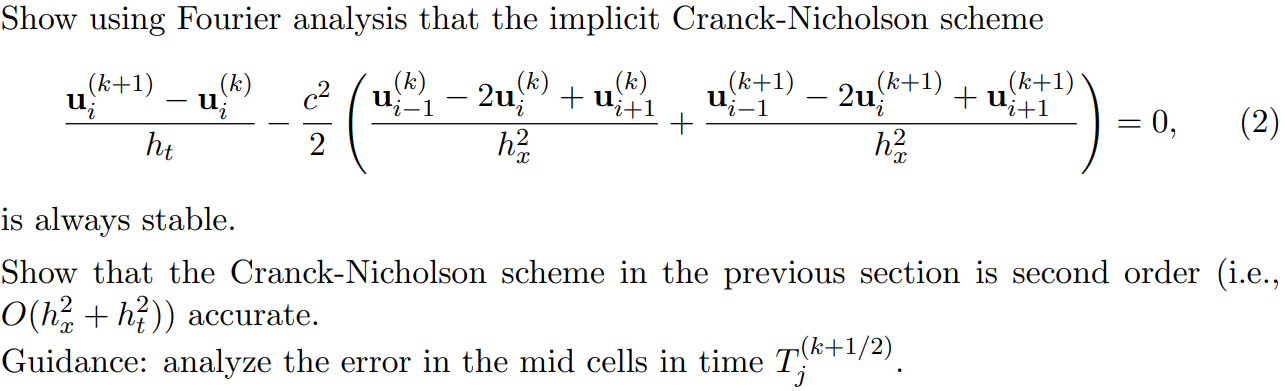
Show using Fourier analysis that the implicit Cranck-Nicholson scheme (k+1) _ uj (k) ( k) Uj_1 - 2u, (k) (k) (k+1) uj + Uit1 (k+1) _ 2uj (K+1 ) i-1 + Uif1 N GO + = 0, ht h2 (2) is always stable. Show that the Cranck-Nicholson scheme in the previous section is second order (i.e., O(ha + he)) accurate. Guidance: analyze the error in the mid cells in time T(k+1/2)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Show using Fourier analysis that the implicit Cranck-Nicholson scheme ( k) (k) (k+1) (K+1) u - Uj C i-1 - 2u, + Uit1 uj-1 + = 0, (2) ht 2 is always stable

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

1. Stability and consistency for the 1-D heat equation (a) Show that the following scheme (Richardson, or LeapFrog) is secondorder accurate, but unconditionally unstable: -._ 202:5 ._ ._ 11.9\"\") =...

The required questions to be answered the last two questions only (Analysis & Conclusion) Fourier Analysis Objectives This lab introduces you to the analysis of complex periodic signals to find the...

3. The Leap-Frog scheme for the wave equation Suppose we are given with the problem (which is the classical wave equation) 321128271 5? baT2=O, 0:33:31. (4) Assume we have Dirichlet boundary...

3. Wireless signal consists of three fundamental properties, which are amplitude, frequency and time. Acoustic wave is a form of wireless signal used in various industries to inspect defects in...

The Leap - Frog scheme for the wave equation Suppose we are given with the problem ( which is the classical wave equation ) d e l 2 u d e l t 2 - b 2 d e l 2 u d e l x 2 = 0 , 0 x 1 . Assume we have...

A voltage-source H-bridge inverter is used to produce the stepped waveform v (t) shown in Figure. For V0 = 50 V, T = 10 msec and D = 0.3: a. Using Fourier analysis, find the amplitude of the...

Consider the stepped voltage waveform of Problem 10.18 and Figure. a. Using Fourier analysis, find the value of D (0 D 0.5) such that the amplitude of the third harmonic component of the voltage...

Manta Ray Company manufactures diving masks with a variable cost of $26. The masks sell for $35. Budgeted fixed manufacturing overhead for the most recent year was $892,400. Actual production was...

Consider Portfolio C in the table return & risk of 3 portfolios E(R) A 0.25 0.27 Portfolio B 0.11 0.08 0.14 0.20 Assuming that the rates of return of the portfolio are normally distributed, what is...

If performance materiality is low, and inherent risk and control risk are high, planned tests of details of balances which the auditor must perform will be high. low. medium. An increase in...

A company is preparing completing their Cash Budget. The following data has been prepared for cash receipts and payments. January February March Cash receipts $1,061,200 $1,182,400 $1,091,700 Cash...