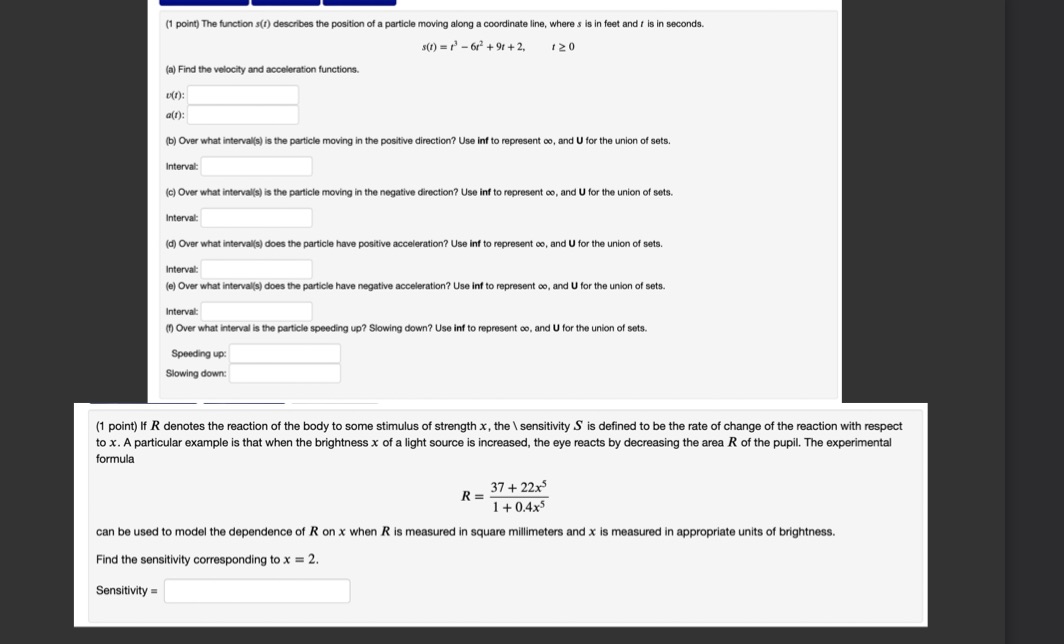
Question: Show work (1 point) The function s(1) describes the position of a particle moving along a coordinate line, where's is in feet and f is
Show work
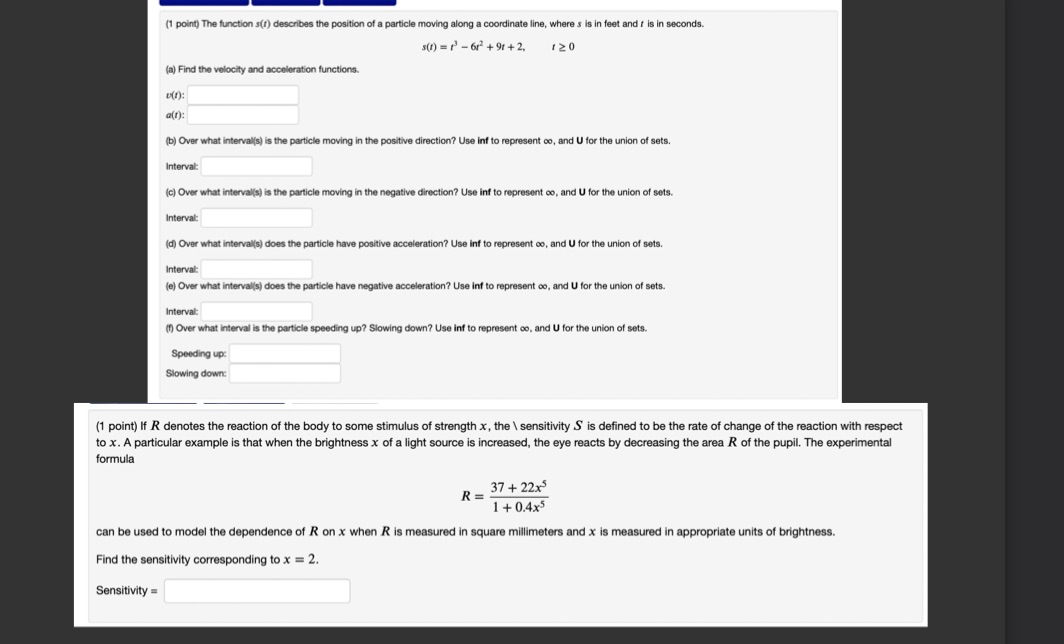
(1 point) The function s(1) describes the position of a particle moving along a coordinate line, where's is in feet and f is in seconds. s(1) = 1 -613 +91 +2, 120 (a) Find the velocity and acceleration functions. ufr): a(f): (b) Over what interval(s) is the particle moving in the positive direction? Use inf to represent co, and U for the union of sets. Interval: (c) Over what intervals) is the particle moving in the negative direction? Use inf to represent co, and U for the union of sets. Interval (d) Over what interval's) does the particle have positive acceleration? Use inf to represent co, and U for the union of sets. Interval: (e) Over what interval(s) does the particle have negative acceleration? Use inf to represent co, and U for the union of sets. Interval (f) Over what interval is the particle speeding up? Slowing down? Use inf to represent co. and U for the union of sets. Speeding up: Slowing down: (1 point) If R denotes the reaction of the body to some stimulus of strength x, the \\ sensitivity S is defined to be the rate of change of the reaction with respect to x. A particular example is that when the brightness x of a light source is increased, the eye reacts by decreasing the area R of the pupil. The experimental formula R = 37+ 22x5 1 + 0.4x5 can be used to model the dependence of R on x when R is measured in square millimeters and x is measured in appropriate units of brightness. Find the sensitivity corresponding to x = 2. Sensitivity =
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


