Show work

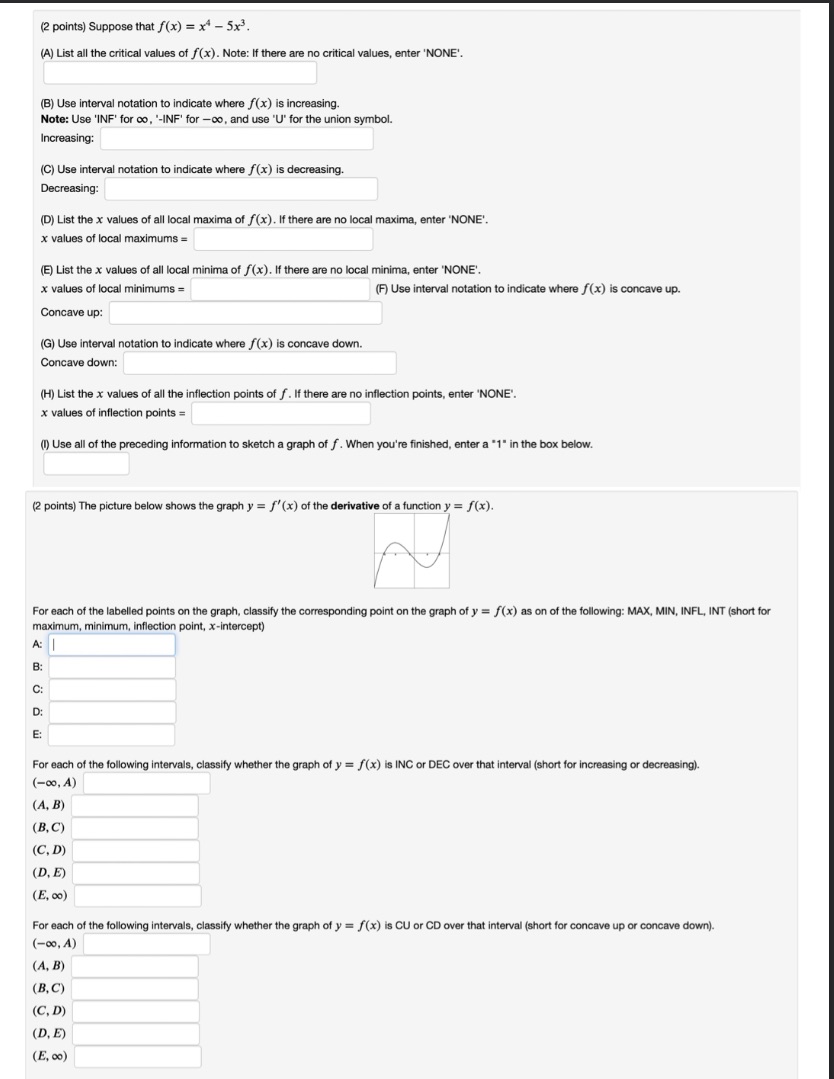
(2 points) Suppose that f(x) = x4 - 5x3 (A) List all the critical values of /(x). Note: If there are no critical values, enter 'NONE'. (B) Use interval notation to indicate where f(x) is increasing Note: Use 'INF' for co, "-INF' for -co, and use "U" for the union symbol. Increasing: (C) Use interval notation to indicate where f(x) is decreasing. Decreasing: (D) List the x values of all local maxima of f (x). If there are no local maxima, enter 'NONE'. x values of local maximums = (E) List the x values of all local minima of f(x). If there are no local minima, enter "NONE'. x values of local minimums = (F) Use interval notation to indicate where f(x) is concave up. Concave up: (G) Use interval notation to indicate where f(x) is concave down. Concave down: (H) List the x values of all the inflection points of f. If there are no inflection points, enter 'NONE'. x values of inflection points = (1) Use all of the preceding information to sketch a graph of f. When you're finished, enter a "1" in the box below. (2 points) The picture below shows the graph y = f'(x) of the derivative of a function y = f(x). For each of the labelled points on the graph, classify the corresponding point on the graph of y = f(x) as on of the following: MAX, MIN, INFL, INT (short for maximum, minimum, inflection point, x-intercept) A: B: C: D: E: For each of the following intervals, classify whether the graph of y = /(x) is INC or DEC over that interval (short for increasing or decreasing). (-00, A) (A, B) (B, C) (C, D) (D, E) (E, 00) For each of the following intervals, classify whether the graph of y = f(x) is CU or CD over that interval (short for concave up or concave down). (-00, A) (A, B) (B, C) (C, D) (D, E) (E, 00)