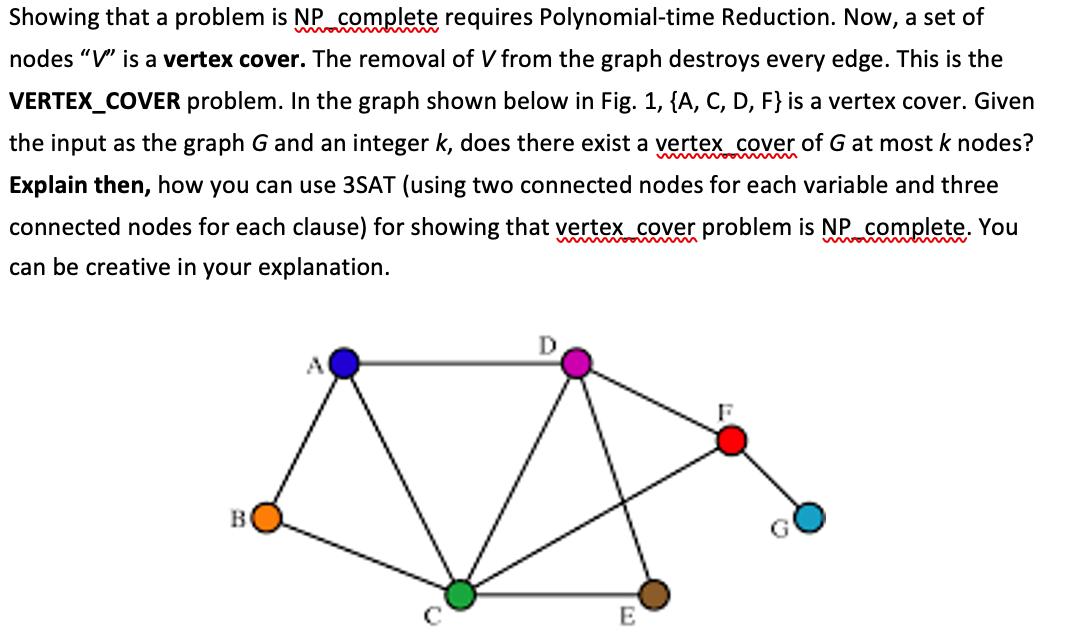
Showing that a problem is NP complete requires Polynomial-time Reduction. Now, a set of nodes "V" is a vertex cover. The removal of V from the graph destroys every edge. This is the VERTEX_COVER problem. In the graph shown below in Fig. 1, {A, C, D, F} is a vertex cover. Given the input as the graph G and an integer k, does there exist a vertex cover of G at most k nodes? Explain then, how you can use 3SAT (using two connected nodes for each variable and three connected nodes for each clause) for showing that vertex cover problem is NP complete. You can be creative in your explanation. B A D E