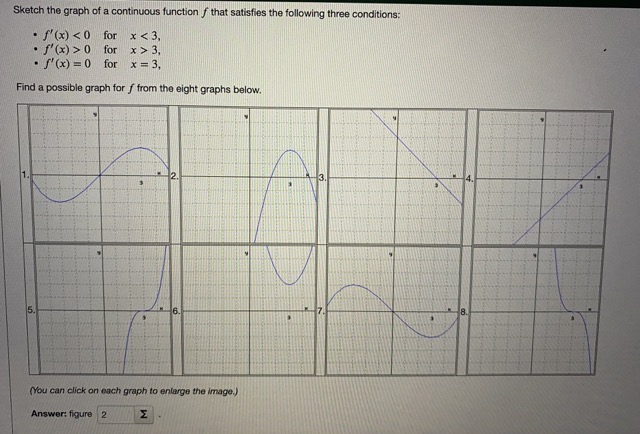
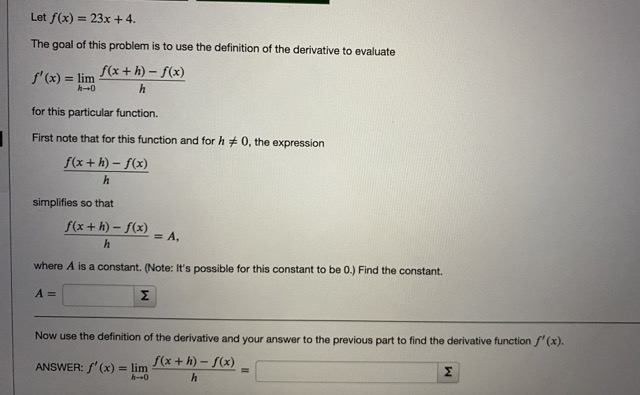
Sketch the graph of a continuous function / that satisfies the following three conditions: . f'(x) 0 for x>3. . f'(x) = 0 for x = 3, Find a possible graph for f from the eight graphs below. (You can click on each graph to enlarge the image.) Answer: figure 2 ELet /(x) = 23x +4. The goal of this problem is to use the definition of the derivative to evaluate f' (x) = lim f(xth) - f(x) h-+0 h for this particular function. First note that for this function and for h # 0, the expression f( x + h) -f(x) h simplifies so that f(x + h) - f(x) = A, where A is a constant. (Note: It's possible for this constant to be 0.) Find the constant. A = Now use the definition of the derivative and your answer to the previous part to find the derivative function / (x). ANSWER: /'(x) = lim S(x+ h) - S(x) I h-+0The goal of this problem is to use the definition of the derivative to find f' (2) = lim f(2 + h) - f(2) h for the function f(x) = 8x-+2. The expression f(2 + h) - f(2) h can be written in the form Ah + B where A and B are constants. Find these constants. A = B = Note: It's possible for one or more of these constants to be 0. Use the definition of the derivative and your answer to the previous part to find S' (2). ANSWER: /' (2) = lim (2 + h) - f(2) I 4-+0 hThe goal of this problem is to use the definition of the derivative to find f' (x) for the function f(x) = 4x2 - 9. First, note that for h # 0, the expression f (x + h) - f(x) h can be written in the form Ax + Bh + C where A, B and C are constants. Find these constants. A = B = C = E Note: It's possible for one or more of these constants to be 0. Now use the definition of the derivative and your answer to the previous part to find the derivative function /" (x). ANSWER: S' (x) = lim /(x + h) - f(x) h Next, use your answer from the previous part to find the value of the derivative function at the indicated point. f'(-4) = E f' (5) =where A, B and C are constants. Find these constants. A= E B = C = E Note: It's possible for one or more of these constants to be 0. Now use the definition of the derivative and your answer to the previous part to find the derivative function f"(x). ANSWER: f' (x) = lim f(x + h) - f(x) h+0 h Next, use your answer from the previous part to find the value of the derivative function at the indicated point. f' (-4) = f' (5) = E Finally, find the slope, m, of the tangent line to the curve y = /(x) at the point (5, f(5)). Answer: m =