Slides 28-30:

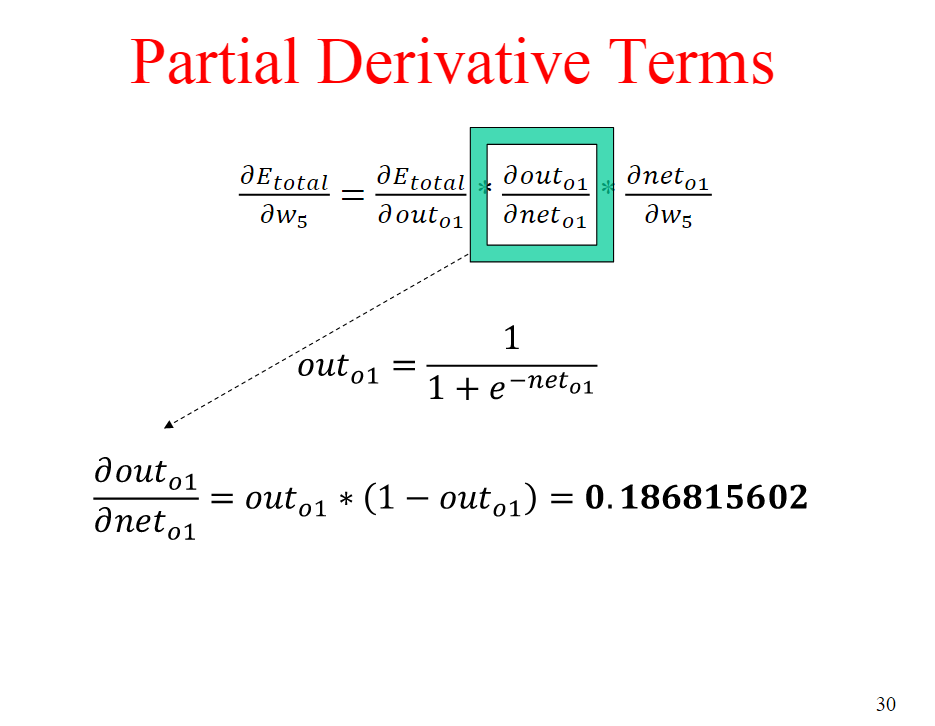
Recall that the sigmoid function has derivative s'(z) = s(2)(l-s(z)). Moreover, recall that during backpro- pogation the derivative s'(z is a factor in the gradient computation used to update the weights of a multilayer perceptron (see slides 28-30 in the neural-nets.pdf slide set). Activation functions like sigmoid have a "satura- tion" problem: when z is very large or very small, s(z) is close to 1 or 0, respectively, and so s'(2 is close to 0. As a result, corresponding gradients will be nearly 0, which slows down training. Affine activation functions with positive slope always have a positive derivative and thus will (more or less) not exibit saturation, but they have other drawbacks (think back to lab 6). Do a little research and find a non-affine activation function that avoids the saturation problem (hint: ReLU). In your own words, describe how this activation is non-affine and also avoids the saturation problem. Briefly dis- cuss any drawbacks your chosen activation function may have, as well as similar alternatives that avoid these drawbacks Recall that the sigmoid function has derivative s'(z) = s(2)(l-s(z)). Moreover, recall that during backpro- pogation the derivative s'(z is a factor in the gradient computation used to update the weights of a multilayer perceptron (see slides 28-30 in the neural-nets.pdf slide set). Activation functions like sigmoid have a "satura- tion" problem: when z is very large or very small, s(z) is close to 1 or 0, respectively, and so s'(2 is close to 0. As a result, corresponding gradients will be nearly 0, which slows down training. Affine activation functions with positive slope always have a positive derivative and thus will (more or less) not exibit saturation, but they have other drawbacks (think back to lab 6). Do a little research and find a non-affine activation function that avoids the saturation problem (hint: ReLU). In your own words, describe how this activation is non-affine and also avoids the saturation problem. Briefly dis- cuss any drawbacks your chosen activation function may have, as well as similar alternatives that avoid these drawbacks