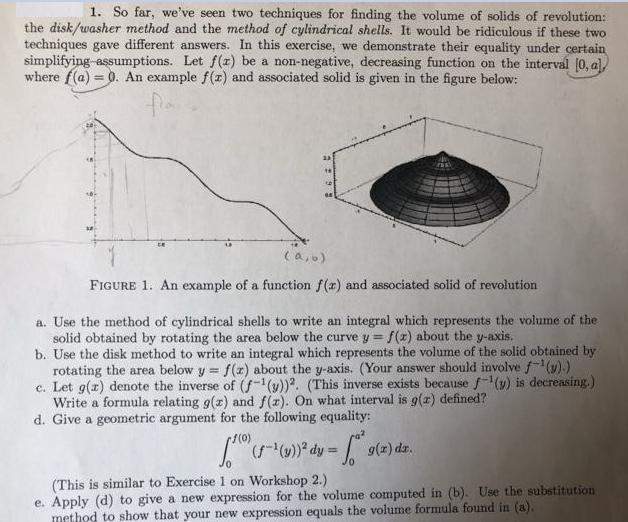
1. So far, we've seen two techniques for finding the volume of solids of revolution: the disk/washer method and the method of cylindrical shells. It would be ridiculous if these two techniques gave different answers. In this exercise, we demonstrate their equality under certain simplifying assumptions. Let f(z) be a non-negative, decreasing function on the interval [0, a] where f(a) = 0. An example f(z) and associated solid is given in the figure below: FIGURE 1. An example of a function f(r) and associated solid of revolution a. Use the method of cylindrical shells to write an integral which represents the volume of the solid obtained by rotating the area below the curve y = f (x) about the y-axis. b. Use the disk method to write an integral which represents the volume of the solid obtained by rotating the area below y = f(x) about the y-axis. (Your answer should involve f-(y).) c. Let g(r) denote the inverse of (f-(y)). (This inverse exists because f-(v) is decreasing.) Write a formula relating g(z) and f(r). On what interval is g(z) defined? d. Give a geometric argument for the following equality: r/(0) ( ()* dy = g(2) dz. !3! (This is similar to Exercise 1 on Workshop 2.) e. Apply (d) to give a new expression for the volume computed in (b). Use the substitution method to show that your new expression equals the volume formula found in (a).