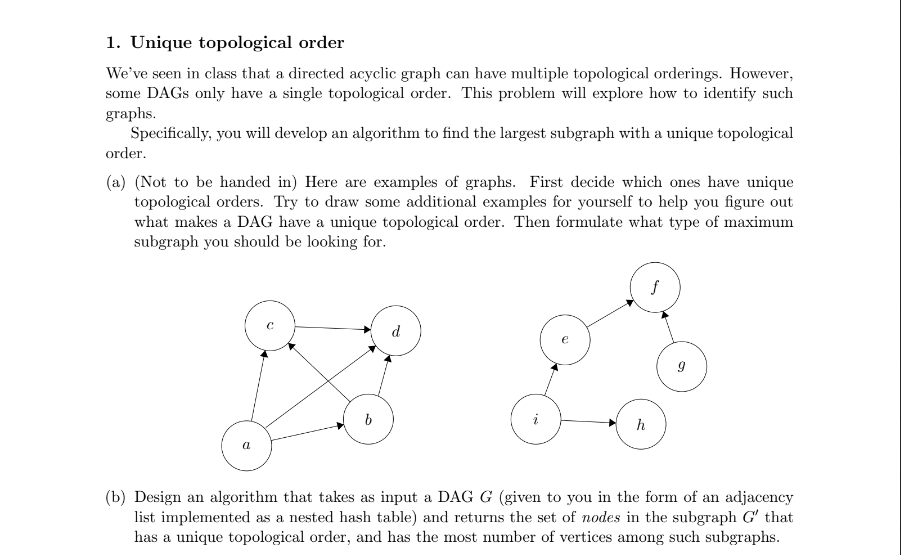
Solution guidelines For problems that require you to provide an algorithm, you must provide: 1. pseudocode and, if helpful, a precise description of the algorithm in English. As always, pseudocode should include A clear description of the inputs and outputs Any assumptions you are making about the input (format, for example) Instructions that are clear enough that a classmate who hasn't thought about the prob- lem yet would understand how to turn them into working code. Inputs and outputs of any subroutines should be clear, data structures should be explained, etc. If the algorithm is not clear enough for graders to understand easily, it may not be graded. 2. a proof of correctness, 3. an analysis of running time and space. You may use algorithms from class as subroutines. You may also use facts that we proved in class. For full credit you need to find the most efficient algorithm. You should be as clear and concise as possible in your write-up of solutions. A simple, direct analysis is worth more points than a convoluted one, both because it is simpler and less prone to error and because it is easier to read and understand. 1. Unique topological order We've seen in class that a directed acyclic graph can have multiple topological orderings. However, some DAGS only have a single topological order. This problem will explore how to identify such graphs. Specifically, you will develop an algorithm to find the largest subgraph with a unique topological order. (a) (Not to be handed in) Here are examples of graphs. First decide which ones have unique topological orders. Try to draw some additional examples for yourself to help you figure out what makes a DAG have a unique topological order. Then formulate what type of maximum subgraph you should be looking for. f S (b) Design an algorithm that takes as input a DAG G (given to you in the form of an adjacency list implemented as a nested hash table) and returns the set of nodes in the subgraph G' that has a unique topological order, and has the most number of vertices among such subgraphs. h 9