Solution is given below can you please explain proper solution why we took. transpose

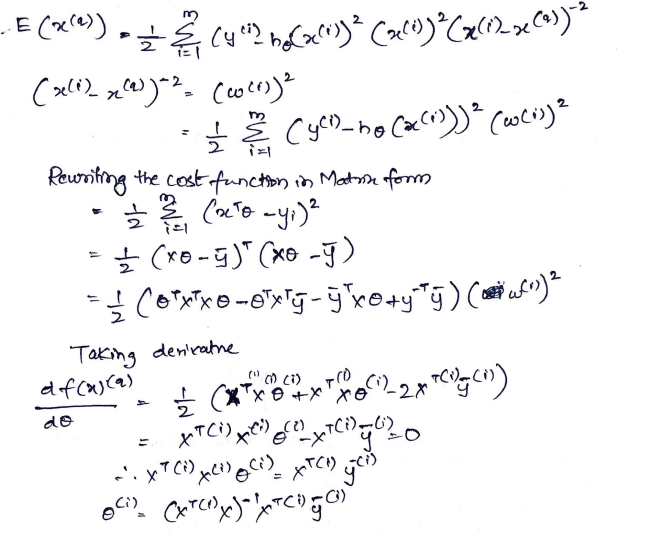
Suppose we want to estimate localized linear regression by weighting the contribution of the data points by their distance to the query point x(q), i.e. using the cost E(x(q))=21i=1m(y(i)h(x(i)))2(x(i)x(q))2 where (x(i)x(q))2=(w(i))2 is the inverse Euclidean distance between the training point x(i) and query (test) point x(q). Derive the modified normal equations for the above cost function E(x(q)). Show all steps. Hint: first, rewrite the cost function in matrix/vector notation, using a diagonal matrix to represent the weights w(i). E(x(i))=21i=1m(y(i)h(x(i))2(x(i))2(x(i)x(i))2(x(i)x(a))2=(w(i))2=21i=1m(y(i)h(x(i)))2((i))2 Rewriting the cost function in Matrix form =21i=1m(xyi)2=21(xy)(xy)=21(xxyyx+yy)((i))2 Taking derivatue ddf(x)(a)=21(xT(i)x(i)(i)+xT(i)x(i)2xT(i)y(i))=xT(i)x(i)(i)xT(i)y(i)=0xT(i)x(i)(i)=xT(i)y(i)