solve.

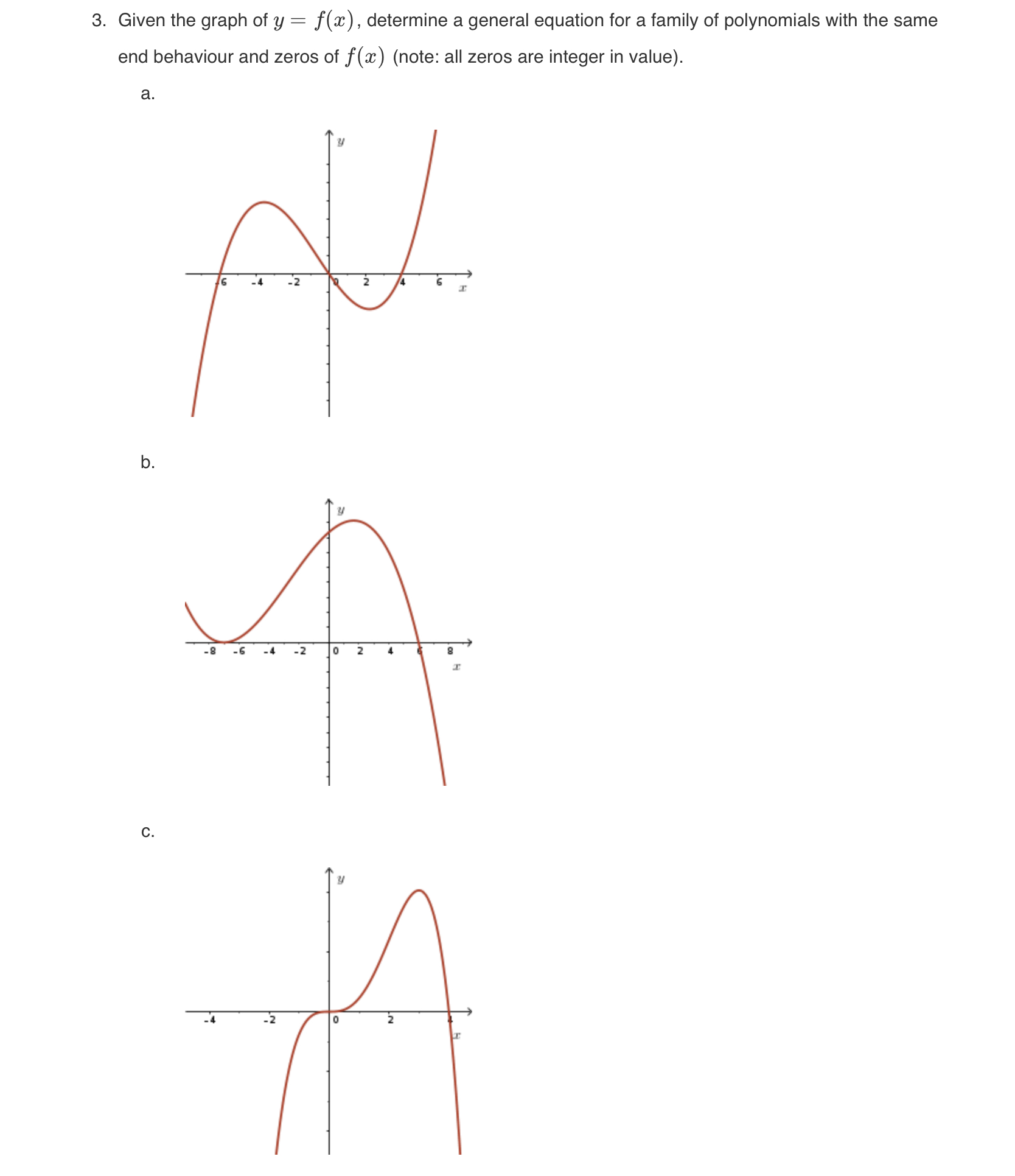
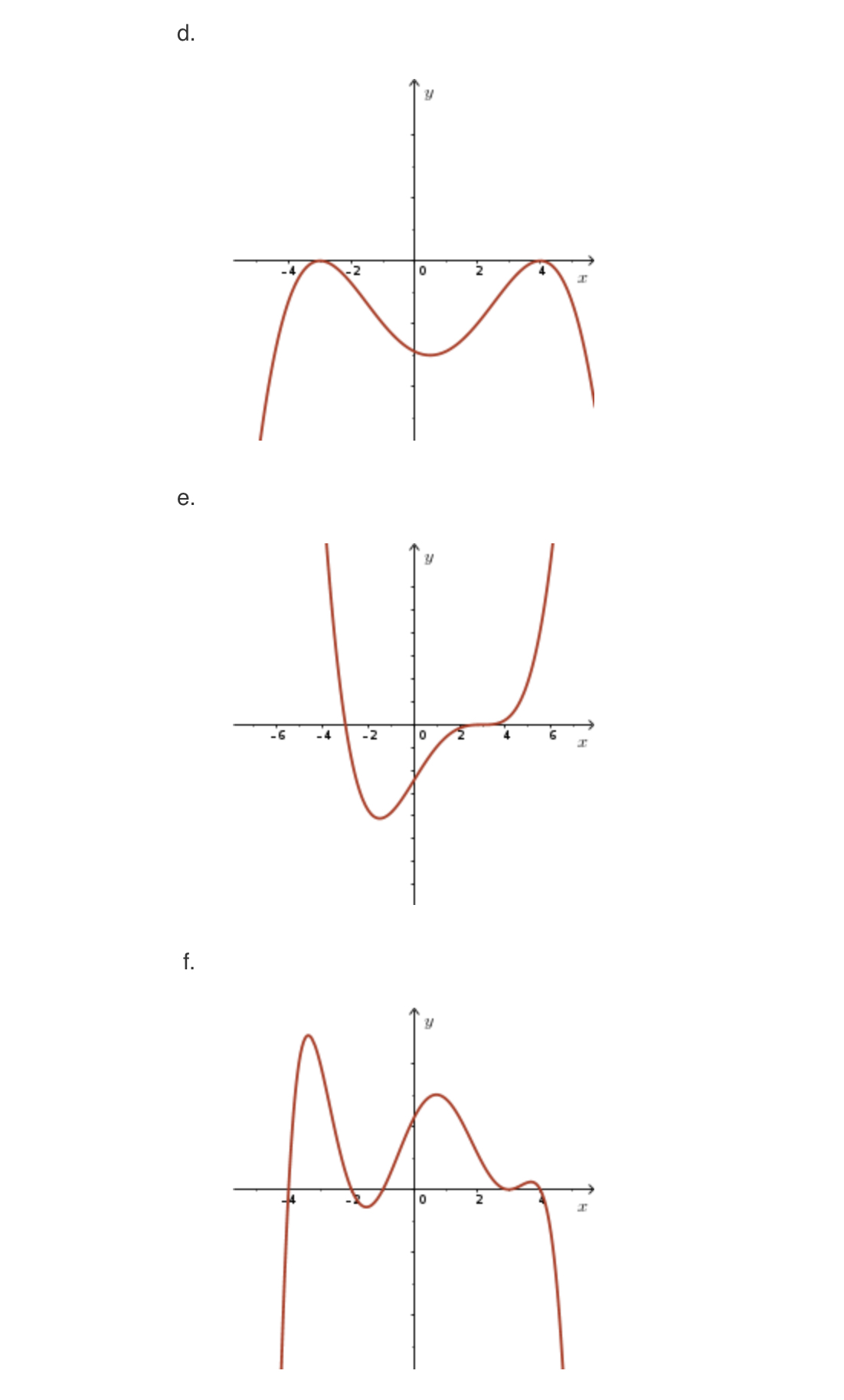
4. State the equation of the quartic function with zeros at : % and 5 (both of multiplicity 1) and a: : 2 (multiplicity 2), having a y-intercept of 4. 3. Given the graph of y : f(:c), determine a general equation for a family of polynomials with the same end behaviour and zeros of f(:c) (note: all zeros are integer in value). a. 8. The function an) : %(;n 2)2(:n + 2)2 has a turning point at (0, 4). Determine a. The intervals where at) is positive and negative. b. The intervals where f(:c) is increasing and decreasing. 9. a. Determine the equation of the cubic function with zeros 1, g, and 3, passing through (4, 5). b. Determine the y-intercept of the function found in part (a) and sketch its graph. 0. State the equation of the cubic function that is a reflection in the x-axis of the function described in part (a). d. Determine algebraically the equation of the cubic function that is a reflection in the y-axis of the function described in part (a). \f2. State the equation of the family of polynomial functions satisfying the following conditions: a. A cubic with zeros x = -3, x = -! 7, and x = Co / CT b. A sixth degree function with zeros x = -2 (order 2), x = 1 (order 1), and x = 5 (order 3). c. A quartic that passes through the origin and has a point of inflection at ( 2, 0) . d. Cubic function, x-intercept at a = -4, a turning point at (1, 0) , and f (ac) > -oo as e. A quartic function with zeros at x = 15 and x = -1 + V2