solve by hands(on paper) please i will uppvote.

.

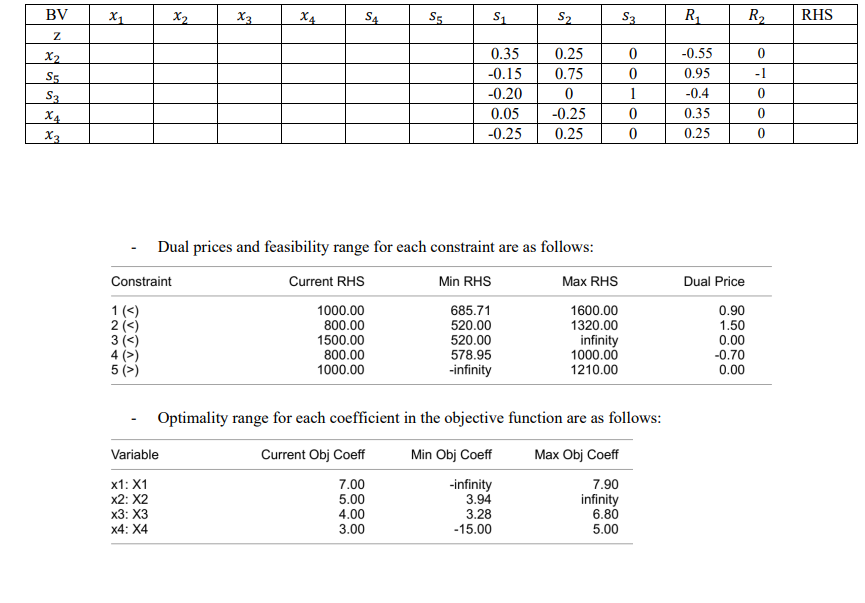
A furniture company manufactures beds, cabinets, desks, and chairs. The manufacture of each type of furniture requires lumber, and three types of skilled labor: carpentry, finishing, and painting. In addition, the company has market requirements of two buyers to satisfy. The production engineer decided to use LP model to optimize the production plan for the company. The production engineer has defined the decision variables as: x1= number of beds produced x2= number of cabinets produced x3= number of desks produced x4= number of chairs produced The production engineer developed the following LP formulation of the problem: Maximize z=7x1+5x2+4x3+3x4 Subject to 2x1+3x2+x3+4x41000 (Carpentry capacity constraint) 5x1+2x2+3x3+x4800 (Finishing capacity constraint) 3x1+x2+x3+2x41500 (Painting capacity constraint) 2x1+x2+2x3+3x4800 (Buyer 1 requirements constraint) x1+2x2+4x3+3x41000 (Buyer 2 requirements constraint) x1,x2,x3,x40 The problem is solved using the Big-M Method (M=100) and the optimal tableau is given below: Where s1,s2, and s3 are the slacks for the carpentry, finishing, and painting capacity constraints, respectively. While s4 and s5 are the surplus variables for the Buyer 1 requirements constraint and Buyer 2 requirements constraint, respectively Based on the given formulation and the given optimal tableau, you are required to prepare a detailed report to: 1. Identify which of the five constraint is binding and which is not binding, showing how you did recognize the constraint state. 2. Find the dual price for each of the five constraints. 3. Find the feasibility range for each dual price. 4. Find the optimality range for each coefficient in the objective function. NOTE: The final answers to the above requirements are given in the next page. 5. Given the following Tableau with B1 provided. Complete the tableau and show your work in detail. - Dual prices and feasibility range for each constraint are as follows: - Optimality range for each coefficient in the objective function are as follows